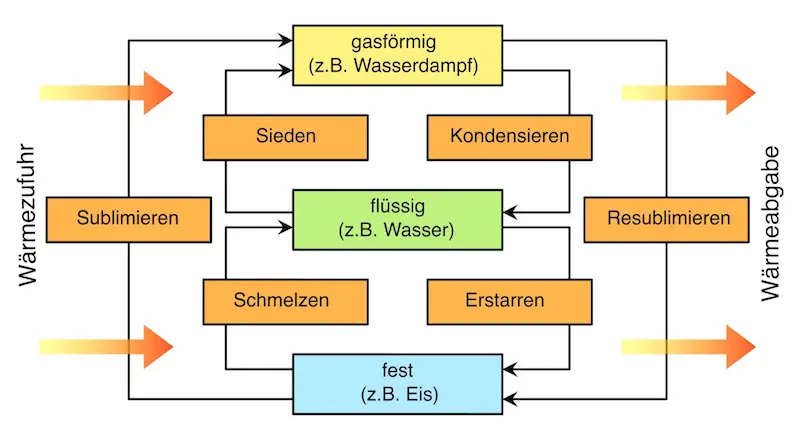
Aggregatzustände und ihre Änderungen

Aggregatzustände

Die unterschiedlichen Zustände eines Stoffes, die sich durch Temperatur-oder Druckänderungen ineinander umwandeln können, bezeichnet man als Aggregatzustände.

Die Umwandlung in einen anderen Aggregatzustand wird auch als Phasenübergang bezeichnet.

Das folgende Schaubild zeigt alle Aggregatzustände und die Umwandlungen, die sich durch Zufuhr bzw. Abgabe von Wärme ergeben:

Um die erforderliche Wärmemenge für die Änderung des Aggregatzustands zu ermitteln, wird folgender Versuch durchgeführt:

Versuch:

Einer bestimmten Menge Eis, welches sich in einem Becherglas befindet, wird mit Hilfe eines Gasbrenners kontinuierlich Energie zugeführt.

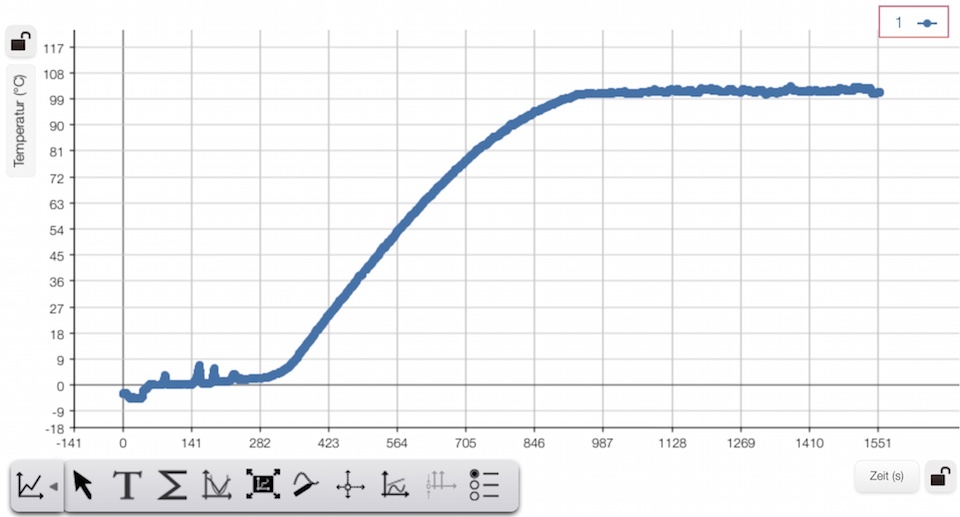
Mit der Zeit schmilzt das Eis, das entstandende Wasser erhitzt sich und fängt schließlich an zu sieden. Im gesamten Zeitraum wird die Temperatur des Eises / des Wassers gemessen und in Abhängigkeit von der Zeit dargestellt.

Beobachtung:

Während der Phasenumwandlungen von fest zu flüssig sowie von flüssig zu gasförmig bleibt die Temperatur weitgehend konstant:

Hinweis:

Die Peaks zu Beginn sind dadurch entstanden, dass nicht genügend gerührt wurde. Dadurch dass bei steigender Temperatur immer mehr Energie an die Umgebung abgegeben wird, ist die Steigung bei der Erwärmung des Wassers nicht ganz konstant sondern wird zum Ende kleiner.

Erklärung:

Bei einer Phasenumwandlung erhöht sich die potentielle Energie der Teilchen. Die gesamte zugeführte Wärme wird für die Phasenumwandlung benötigt – die Temperatur bleibt daher konstant.

Die Energie, die zum Schmelzen bzw. zum Verdampfen eines Stoffes notwendig ist, bezeichnet man als Schmelzwärme (Schmelzenergie) bzw. Verdampfungswärme (Verdampfungsenergie).

Bestimmung der Schmelzwärme und Verdampfungswärme von Eis bzw. Wasser

Um zu bestimmen, wie viel Energie zum Schmelzen des Eises bzw. zum Verdampfen des Wassers benötigt wurde, müssen wir zunächst ermitteln, wie viel Energie der Gasbrenner an das Eis / Wasser in einer bestimmten Zeit abgibt. Damit lässt sich dann aus den Zeitspannen die zugeführte Wärmeenergie berechnen.

Die vom Gasbrenner abgegebene Energie lässt sich aus der Temperaturkurve und der spezifischen Wärmekapazität von Wasser ermitteln:

Wir lesen ab, in welcher Zeitspanne $\Delta t$ eine bestimmte Temperaturänderung $\Delta \vartheta$ erfolgt ist.

Aus dem Diagramm erhält man z.B.:

Der Anstieg von 12 °C auf 50 °C dauerte ca. 184 s. Damit ist $\Delta \vartheta=38\, K$ und $\Delta t=184\, s$ .

Die Masse des Eises (bzw. des Wassers) betrug $m=141\, g$ .

Mit Hilfe der Grundgleichung der Wärmelehre $Q=c\cdot m\cdot \Delta T$ lässt sich die Energie berechnen, die notwendig ist, um 141 g Wasser um 38 K zu erwärmen:

$Q=4,19\, \frac {J}{gK}\cdot 141\, g\cdot 38\, K=22.450\, J$

Diese Energie hat der Gasbrenner in 184 Sekunden abgegeben.

Die pro Sekunde abgegebene Wärmenergie beträgt damit

$Q=\dfrac {22.450\, J}{184}=122\, J$ (Der Brenner erzeugt also eine Wärmeleistung von 122 W.)

Schmelzwärme

Die Dauer des Schmelzprozesses lässt sich aus dem Diagramm abschätzen:

Der Schmelzprozess dauerte ca. 260 Sekunden.

In dieser Zeit hat der Gasbrenner die Energie $122\, \frac {J}{s}\cdot 260\, s=31.720\, J$ abgegeben.

Die Schmelzwärme beträgt damit $Q_{s}=31.720\, J$ .

Aus der Masse des Eises (m = 141 g) lässt sich die Schmelzwärme für 1 g Eis berechnen. Dies ist die spezifische Schmelzwärme.

Spezifische Schmelzwärme q_s von Wasser: $q_{s}=\dfrac {31.720\, J}{141\, g}=225\, \frac {J}{g}$ .

Der Literaturwert für die spezifische Schmelzwärme von Eis beträgt $q_{s}=334\, \frac {J}{g}$ .

Das bedeutet:

Um 1 g Eis zum Schmelzen zu bringen wird eine Energie von q_s = 334 J benötigt. Die Temperatur ändert sich dabei nicht.

Verdampfungswärme

Durch Bestimmung der Masse des nicht verdampften Wassers nach dem Versuch lässt sich die Masse des verdampften Wassers bestimmen.

Diese betrug in unserem Versuch 48 g.

Die Zeit, in der das Wasser verdampfte, lässt sich aus dem Diagramm abschätzen.

Sie betrug ca. 630 Sekunden.

In dieser Zeit hat der Gasbrenner die Energie $122\, \frac {J}{s}\cdot 630\, s=76.860\, J$ abgegeben.

Damit beträgt die Verdampfungswärme $Q_{v}=76.860\, J$ .

Auf ein Gramm umgerechnet ergibt sich die spezifische Verdampfungswärme q_v von Wasser:

Spezifische Verdampfungswärme q_v von Wasser: $q_{v}=\dfrac {76.860\, J}{48\, g}=1.601\, \frac {J}{g}$ .

Der Literaturwert für die spezifische Verdampfungswärme von Wasser beträgt $q_{v}=2.256\, \frac {J}{g}$ .

Fehlerquellen:

Die ermittelten Werte liegen jeweils deutlich unter dem Literaturwert.

Die Hauptgründe dafür sind:

Das Eis nimmt auch aus der Umgebung Wärme auf.
Die Energieabgabe des Gasbrenners ist nicht konstant sondern umso größer, je kälter der zu erwärmende Stoff ist.
Bei steigender Temperatur gibt das Wasser immer mehr Wärme an die Umgebung ab.
Bereits vor dem Erreichen der Temperatur von 100 °C verdampft ein Teil des Wassers.

weiter mit Gasgesetze und Gasgleichung

zurück