Das optische Gitter - Interferenz am optischen Gitter

Vom Doppelspalt zum optischen Gitter

Der Doppelspalt, mit dem wir bereits die Wellenlänge von Licht bestimmt haben, hat zwei große Nachteile:

Es geht nur sehr wenig Licht hindurch, was vor allem mit einer gewöhnlichen Lichtquelle zu einem sehr lichtschwachen Muster führt.
Die Maxima sind nicht scharf – die Intensität geht von einem Maximum zu einem Minimum nur allmählich zurück

Beide Nachteile lassen sich mit einem Mehrfachspalt beseitigen. Einen solchen Mehrfachspalt nennt man auch optisches Gitter.

Ein optisches Gitter besteht aus sehr vielen nebeneinanderliegenden Spalten, die jeweils den gleichen Abstand zueinander haben. Der Spaltabstand wird wie beim Doppelspalt mit g bezeichnet. Diesen Abstand bezeichnet man als Gitterkonstante.

Bei gleichem Spaltabstand entspricht das Interferenzmuster eines optischen Gitters dem des Doppelspalts, die Maxima sind jedoch heller und schärfer (die Dunkelstellen sind breiter):

^{Beugungsbild eines optischen Gitters mit 40 Strichen pro cm}

^{Beugungsbild eines optischen Gitters mit 100 Strichen pro cm}

Die größere Helligkeit entsteht dadurch, dass mehrere Spalte beleuchtet werden, wodurch mehr Licht zum Schirm gelangt.

Doch warum sind die Maxima schärfer und die Dunkelstellen so breit?

Interferenz von Licht am optischen Gitter

Um zu verstehen, warum die Dunkelstellen breiter sind, es also an mehreren Stellen auf dem Schirm zur völligen Auslöschung kommt, betrachten wir zunächst die Teilstrahlen aus mehreren Spalten, die zu einem Maximum führen, etwas genauer:

Durch jeden Spalt tritt Licht, welches im Maximum konstruktiv interferiert. Wie beim Doppelspalt entsteht ein Maximum, wenn der Gangunterschied zwischen zwei benachbarten Teilstrahlen dem ein- oder vielfachen der Wellenlänge entspricht, wenn also gilt:

$\delta=k\cdot \lambda$

Für das Maximum 1. Ordnung gilt:

Der Gangunterschied zwischen zwei Teilstrahlen beträgt jeweils

$\delta=\lambda$

Zwischen dem 1. und 3. Teilstrahl (also zum übernächsten Teilstrahl) beträgt der Gangunterschied

$\delta=2\lambda$ ,

Zwischen dem 1. und k-ten Teilstrahl gilt:

$\delta_{k}=(k-1) \cdot \lambda$

Zwischen allen benachbarten Teilstrahlen besteht der gleiche Gangunterschied, (nämlich δ = λ), daher kommt es für alle Teilstrahlen im gleichen Punkt P zur maximalen Verstärkung.

Bereits kleine Gangunterschiede führen zur Auslöschung

Betrachten wir nun einen Punkt, der ein kleines Stück oberhalb des Maximums erster Ordnung liegt – der Gangunterschied zwischen zwei benachbarten Teilstrahlen, die zu diesem Punkt gelangen, ist nun ein wenig größer als eine Wellenlänge.

Nehmen wir an, der Gangunterschied zwischen zwei benachbarten Teilstrahlen beträgt

$\delta=1,1\lambda$

Ein Gangunterschied von δ = 1,1λ zwischen zwei Teilstrahlen würde normalerweise immer noch zu einer Verstärkung führen. Erst bei einem Gangunterschied von δ = 1,5λ würde es zur kompletten Auslöschung kommen.

Aber es gibt ja noch viele weitere Teilstrahlen:

In unserem Beispiel kommt es zwischen dem 1. und 3.Teilstrahl bereits zu einem Gangunterschied von

$\delta=2,2\lambda$ ,

zwischen dem 1. und 4. Teilstrahl gilt

$\delta=3,3\lambda$ ,

zwischen dem 1. und 5. Teilstrahl

$\delta=4,4\lambda$ ,

und zwischen dem 1. und 6. Teilstrahl beträgt der Gangunterschied

$\delta=5,5\lambda$ .

Für den 1. und 6. Teilstrahl ist also die Bedingung für komplette Auslöschung erfüllt!

Nun gibt es aber noch eine Vielzahl weiterer Teilstrahlen.

Ein Gangunterschied von $\delta=5,5\lambda$ besteht ebenfalls

→ zwischen dem 2. und 7. Teilstrahl

→ zwischen dem 3. und 8. Teilstrahl

→ zwischen dem 4. und 9. Teilstrahl

usw.

Ist die Anzahl der Teilstrahlen groß genug, findet man also praktisch für jeden Teilstrahl einen Partner, mit dem dieser destruktiv interferiert.

Je größer die Anzahl der beleuchteten Spalte ist (je kleiner also die Gitterkonstante), desto schärfer werden die Maxima, denn dann führt bereits jede noch so kleine Abweichung von der Bedingung für maximale Verstärkung zwischen zwei benachbarten Teilstrahlen (also z.B. δ = 1,01λ) zu einer vollständigen Auslöschung.

Ein kleiner Spaltabstand führt zu großen Abständen zwischen Maxima

Der Abstand der Maxima ist umso größer, je kleiner die Gitterkonstante (also je kleiner der Abstand zwischen den Spalten) ist. Es lassen sich optische Gitter mit mehreren Hundert Strichen pro Millimeter herstellen. Die Gitterkonstante ergibt sich aus dem Kehrwert dieser Anzahl pro mm.

Beispiel: Bei 100/mm beträgt die Gitterkonstante g = 1/100mm = 10μm.

Mit dem Spaltabstand wird natürlich auch die maximale Spaltbreite begrenzt – schließlich muss jeder Spalt schmaler sein als der Abstand der Spaltmittelpunkte. Beim Doppelspalt mit nur zwei Spalten würde dann aber so wenig Licht hindurch gehen, dass das Beugungsbild kaum sichtbar wäre.

Ein großer weiterer großer Vorteil des optischen Gitters ist also der kleine mögliche Spaltabstand, der zu großen Abständen zwischen den Maxima führt.

Hier verschiedene Beugungsbilder von optischen Gittern mit kleiner Gitterkonstante:

^{Beugungsbild mit optischem Gitter – Lichtquelle: Laser}

^{Beugungsbild mit optischem Gitter – Lichtquelle: Glühlampe}

Mit einer gewöhnlichen Lichtquelle entsteht ein helles Hauptmaximum und farbige Spektren in den Maxima höherer Ordnung.

Da alle Lichtfarben kontinuierlich ohne Unterbrechungen ineinander übergehen, spricht man von einem kontinuierlichen Spektrum.

Mit einem sogenannten “Rowland Gitter” (570 Striche pro mm) entsteht folgendes Beugungsbild einer weißen Lichtquelle:

^{Gitterspektrum einer Glühlampe}

Die Maxima sind noch breiter als im oberen Bild, so dass das Spektrum des enthaltenen Lichts noch besser zu erkennen ist. Der Bereich zwischen rot und grün ist orange / gelb, was auf dem Foto leider nicht zu erkennen ist. Im Hauptmaximum in der Mitte interferieren alle Lichtfarben konstruktiv (hier ist der Gangunterschied 0), daher ist dieses weiß.

Da man mit einem solchen Gitter das Licht in seine Bestandteile zerlegen und analysieren kann, spricht man auch von einem Gitterspektrometer.

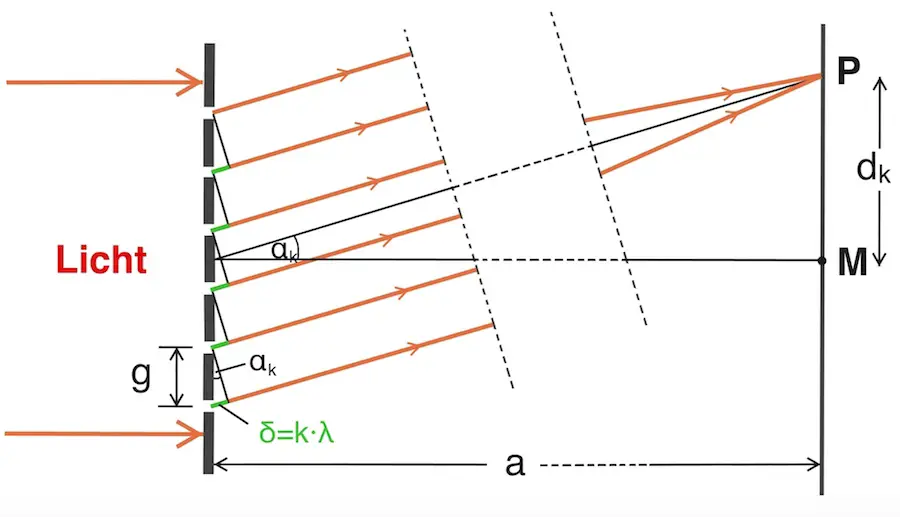
Die gleichen Zusammenhänge, die wir schon für den Doppelspalt hergeleitet haben, gelten auch für das optische Gitter.

Es gilt (s. Skizze oben):

$\dfrac {\delta}{g}=sin\alpha$ und $\dfrac {d}{a}=tan\alpha$

Bei kleinem Spaltabstand liegen die Maxima jedoch so weit voneinander entfernt, dass der Winkel α deutlich größer ist als 1°.

Deswegen ist die Vereinfachung sin α = tan α hier nicht mehr zulässig.

Möchte man beispielsweise die Wellenlänge bei bekannter Gitterkonstanten berechnen, muss man zunächst mit Hilfe des Zusammenhangs

$\dfrac {d}{a}=tan\alpha$

den Winkel $\alpha$ berechnen und diesen dann in die Formel

$\dfrac {\delta}{g}=sin\alpha$ bzw. $\dfrac {\lambda}{g}=sin\alpha$

einsetzen.

Eine andere Möglichkeit zur genauen Berechnung der Wellenlänge ist, im großen Dreieck (vgl. Bestimmung der Wellenlänge von Licht) die unbekannte Hypotenuse mit Hilfe des Pythagoras auszudrücken. Diese hat somit die Länge $\sqrt{a^{2}+d^{2}}$ .

Damit ergibt sich im großen Dreieck

$\dfrac {d}{\sqrt {a^{2}+d^{2}}}=\sin \alpha$

Somit lassen sich beide Gleichungen gleichsetzen, und man erhält für die Wellenlänge

$\lambda=\dfrac {g\cdot d}{\sqrt {a^{2}+d^{2}}}$ bzw. $k\, \lambda =\dfrac {g\cdot d_{k}}{\sqrt {a^{2}+d^{2}_{k}}}$

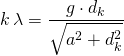
Optische Gitter, die das Licht durchlassen, nennt man Transmissionsgitter.

Daneben gibt es auch optischer Gitter, die das Licht reflektieren.

Ein Beispiel für ein solches Reflexionsgitter findest Du im nächsten Abschnitt!

weiter mit CD als optisches Gitter

zurück