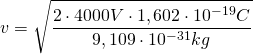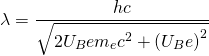Die berechnete Wellenlänge liegt im Bereich der Röntgenstrahlung. Um Welleneigenschaften von Elektronen mit entsprechender kinetischer Energie nachzuweisen, müssten also Methoden gewählt werden, die sich auch zum Nachweis der Welleneigenschaften von Röntgenstrahlen eignen – z.B. also mit Hilfe von Kristallen.
Experimentelle Bestätigung
Tatsächlich lieferten knapp vier Jahre später, im Jahre 1927, die Amerikaner C. J. Davisson und L. H. Germer den experimentellen Nachweis für die Welleneigenschaften von Elektronen mit Hilfe eines Nickelkristalls. Sie konnten dabei auch die von De Broglie postulierte Wellenlänge bestätigen.
Ein ähnliches Verfahren, bei dem kein Einkristall sondern eine dünne Schicht kleiner Graphitkristalle verwendet wird, liefert ebenfalls eine Bestätigung der postulierten Welleneigenschaften. Dieses zunächst zur Interferenz von Röntgenstrahlung genutzte Verfahren nennt sich Debye-Scherrer-Verfahren.
Dieses Verfahren lässt sich mit Hilfe einer Elektronenbeugungsröhre realisieren:
Auf der durchbohrten Anode einer Elektronenstrahlröhre ist eine dünne Schicht mit Graphitkristallpulver aufgebracht. Nachdem der gebündelte Elektronenstrahl diese Schicht durchdrungen hat, trifft er auf einen Leuchtschirm.
Beobachtung:
Auf dem Leuchtschirm entsteht ein kreisförmiges Bild mit einer hellen Mitte und zwei deutlich voneinander getrennten hellen Ringen:
 Interferenzmuster in Form von konzentrischen Kreisen
Interferenzmuster in Form von konzentrischen Kreisen
Verändert man die Beschleunigungsspannung, so zeigt sich:
Die Ringe werden umso kleiner, je größer die Beschleunigungsspannung ist.
Erklärung:
Wenn Teilchen, wie Elektronen, an der Graphitschicht gestreut werden, sollte eigentlich in der Mitte des Leuchtschirms ein heller Kreis entstehen, der nach außen hin dunkler wird.
Bei den Ringen handelt es sich jedoch um Interferenzerscheinungen. Die „Elektronenwellen“ werden wie Röntgenstrahlen an den verschiedenen Netzebenen der Mikrokristalle reflektiert und interferieren je nach Winkel, in dem sie auf die Kristalle treffen, konstruktiv oder destruktiv.
Mit der Bragg-Gleichung lässt sich die Wellenlänge der Elektronenwellen berechnen (der Glanzwinkel ergibt sich aus den Radien der Ringe auf dem Schirm und dem bekannten Netzebenenabstand von Graphit). Diese stimmt mit der berechneten De-Broglie-Wellenlänge überein.
Damit können die Welleneigenschaften sowie die von De Broglie postulierte Wellenlänge von Elektronen bestätigt werden.
Die De-Broglie-Wellenläge der Elektronen hängt vom Impuls und damit von der Beschleunigungsspannung ab. Je größer die Beschleunigungsspannung, umso größer der Impuls und umso kleiner die Wellenlänge.
Das erklärt den beobachteten Zusammenhang zwischen Beschleunigungsspannung und Radius der Ringe: Je größer die Beschleunigungsspannung, umso kleiner die Wellenlänge und umso kleiner der Radius.
![]() den Impuls
den Impuls ![]() zuordnen kann, ergibt sich im Umkehrschluss, dass man einem Elektron mit dem Impuls p die Wellenlänge
zuordnen kann, ergibt sich im Umkehrschluss, dass man einem Elektron mit dem Impuls p die Wellenlänge ![]() zuordnen kann.
zuordnen kann.