Inertialsysteme und Relativitätsprinzip

Inertialsysteme

In der speziellen Relativitätstheorie geht es darum, wie Ereignisse in einem Inertialsystem von einem anderen Inertialsystem aus beobachtet und gemessen werden.

Unter einem Inertialsystem versteht man ein Bezugssystem, in dem das erste Newtonsche Axiom (Trägheitsgesetz) gilt:

Wenn auf einen Körper keine Kraft wirkt, so verharrt er in Ruhe oder in gleichförmiger linearer Bewegung. Rotierende oder anderweitig beschleunigte Bezugssysteme sind keine Inertialsysteme. In ihnen treten Scheinkräfte auf, und daher gilt in ihnen das erste Newtonsche Axiom nicht.

Streng genommen ist auch die Erde kein Inertialsystem, da sie rotiert. Wir können sie jedoch in den meisten Fällen näherungsweise als Inertialsystem betrachten.

Das Relativitätsprinzip

Ein Bezugssystem, das sich relativ zu einem Inertialsystem mit konstanter Geschwindigkeit bewegt, ist ebenfalls ein Inertialsystem.

Wenn wir Beobachtungen oder Messungen in einem Inertialsystem vornehmen, bedeutet das, dass wir uns darin in Ruhe befinden.

Alle Körper verhalten sich in allen Inertialsystemen gleich – so bemerken wir keinen Unterschied, wenn wir die Bewegung eines Körpers untersuchen, ob wir uns in einem (gleichförmig) fahrenden Zug oder in einem bezüglich der Erde ruhenden Bezugssystem befinden.

Diesem Prinzip waren sich sowohl Galileo als auch Newton bewusst, inzwischen wird es als Relativitätsprinzip bezeichnet.

Das bedeutet: Die Grundgesetze der Physik sind in allen Inertialsystemen gleich.

Wenn man in einem mit konstanter Geschwindigkeit fahrenden Zug läuft, einen Kaffee trinkt, einen Körper fallen lässt oder Tischtennis spielt, so verhalten sich alle Körper genauso wie in einem bezüglich der Erde ruhenden Bezugssystem. Ein fallender Körper fällt senkrecht hinunter, wie wir es von der Erde aus gewohnt sind.

Beobachtet man jedoch einen Körper, der sich in einem Inertialsystem in Ruhe befindet, sich gleichförmig in eine bestimmte Richtung bewegt oder frei fällt, aus einem anderen sich zum ersten relativ bewegten Inertialsystem, so wird man dort eine andere Bewegung wahrnehmen.

Beispiel:

Auf dem Bahnsteig nimmt man einen im Zug sitzenden Fahrgast als gleichförmig bewegt wahr, solange der Zug sich mit konstanter Geschwindigkeit bewegt. Der Fahrgast befindet sich im Bezugssystem Zug jedoch in Ruhe.

Ein im Zug frei fallender Körper bewegt sich für den Beobachter im Zug senkrecht nach unten, beschreibt jedoch für den Beobachter auf dem Bahnhof eine Parabelbahn (Wurfparabel).

Erklärung: Ein Beobachter in einem Inertialsystem sieht das Resultat der Überlagerung der Bewegung eines Objektes in einem anderen Inertialsystem mit der relativen Bewegung des Inertialsystems selbst.

Beim Übergang von einem Inertialsystem in ein anderes bleiben die Größen , oder unverändert. Man bezeichnet solche Größen als invariant. In allen Inertialsystemen gelten die gleichen Gesetze der Mechanik. Eine wichtige Schlussfolgerung lautet daher:

Alle Inertialsysteme sind gleichberechtigt (äquivalent). In ihnen gelten die gleichen physikalischen Gesetze.

Kein Inertialsystem ist also in irgendeiner Weise besser als ein anderes. Eine Person, die in einem fliegenden Flugzeug sagt, sie wäre in Ruhe, hat damit genauso recht wie eine sich auf der Erde befindende Person, die von sich selbst behauptet, in Ruhe zu sein. Es ist nicht möglich, ein Bezugssystem auszuwählen, welches sich in absoluter Ruhe befindet.

Galilei-Transformation

Die Gleichungen, mit denen sich die räumlichen und zeitlichen Koordinaten eines Punktes von einem Inertialsystem in ein anderes umrechnen lassen, werden als Galilei-Transformation bezeichnet.

Beispiel:

Ein Zug (Inertialsystem S’) bewegt sich bezüglich eines Beobachters auf dem Bahnsteig (Inertialsystem S) in x-Richtung mit konstanter Geschwindigkeit v.

Zum Zeitpunkt t = t’ = 0 ist auch x = x’ = 0.

Betrachtet man einen Punkt P, so ist dieser zur Zeit t im System S durch die Koordinaten x, y, z charakterisiert.

Innerhalb der Zeitspanne hat sich das System um die Strecke weiterbewegt (unteres Bild).

Zur Zeit gilt also für die Koordinaten von P in Bezugssystem S:  .

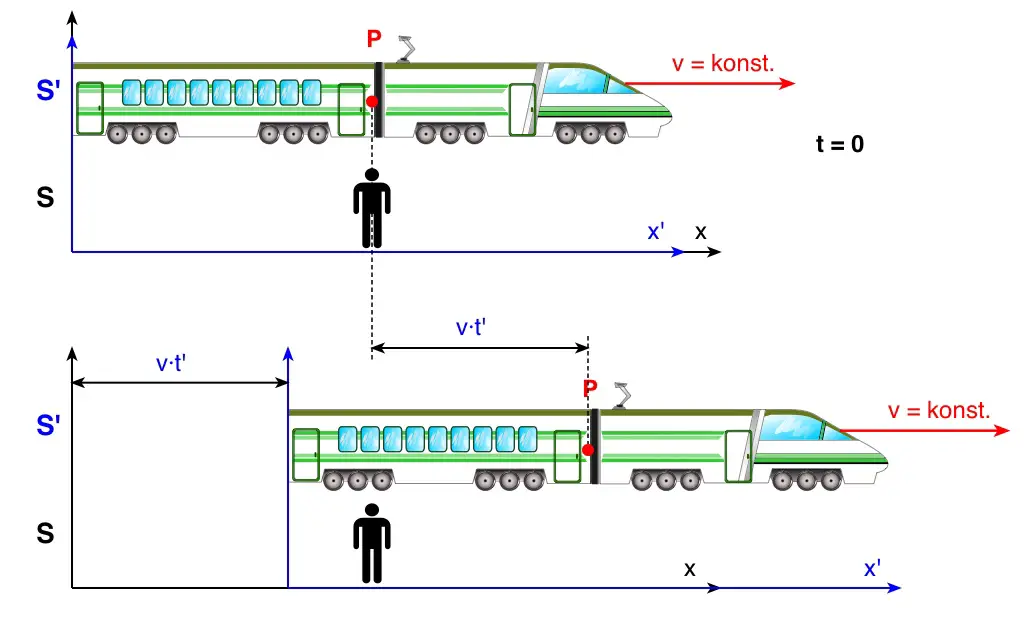
Da die Bewegung entlang der x-Achse erfolgt, bleiben die y- und z-Koordinaten unverändert. Da die Zeit in der Galilei-Newtonschen Physik als absolut angenommen wird, gilt .

So ergibt sich die Galilei-Transformation:

Umrechnung von von S’ nach S

Umrechnung von S nach S’

Bewegt sich der Punkt P innerhalb des Inertialsystems in x-Richtung mit einer Geschwindigkeit  , so beträgt seine Geschwindigkeit in System   . Die Geschwindigkeiten in die Raumrichtung y und z bleiben unverändert.

Die in gemessene Geschwindigkeit entspricht also der Summe aus der Geschwindigkeit des Punktes in und der Geschwindigkeit des Systems bezüglich .

Die Relativgeschwindigkeit zweier Körper ist jedoch unabhängig vom Bezugssystem (invariant).

Invariant: Zeit, Länge, Beschleunigung, Masse, Kraft

Nicht invariant: Weg, Geschwindigkeit

Absoluter Raum und Äther

Die Maxwell-Gleichungen (1861-1864) sagten die Existenz elektromagnetischer Wellen mit der Ausbreitungsgeschwindigkeit  voraus.

Die Frage war jedoch: In welchem Bezugssystem gilt diese Geschwindigkeit? Man hat angenommen, dass für Licht die gleichen Umrechnungen der Galilei-Transformation gelten wie für bewegte Körper.

Außerdem nahm man an, dass elektromagnetische Wellen wie Wasserwellen oder Schallwellen ein Ausbreitungsmedium benötigten. Luft konnte es nicht sein – denn schließlich gelangt das Licht von der Sonne durch den luftleeren Raum zur Erde.

Lange Zeit war man davon überzeugt, dass ein Stoff, den man Äther nannte, den gesamten Raum durchdringt und als Träger für elektromagnetische Wellen dient. Allerdings führte diese Annahme zu Widersprüchen mit den Maxwell-Gleichungen.

In einem Experiment, welches oft als Startschuss für die Relativitätstheorie gilt, sollte der ruhende Äther bzw. die Geschwindigkeit des Äthers gegenüber der Erde nachgewiesen werden. Die Rede ist vom Michelson-Morley-Experiment.