Ermittlung der Geschwindigkeit in Abhängigkeit von der Zeit
Die Geschwindigkeit eines harmonischen Oszillators ändert sich ständig. Dabei gilt:
- Am größten ist die Geschwindigkeit in der Gleichgewichtslage.
- In den Umkehrpunkten ist die Geschwindigkeit 0.
- In den Umkehrpunkten kehrt sich das Vorzeichen der Geschwindigkeit um.
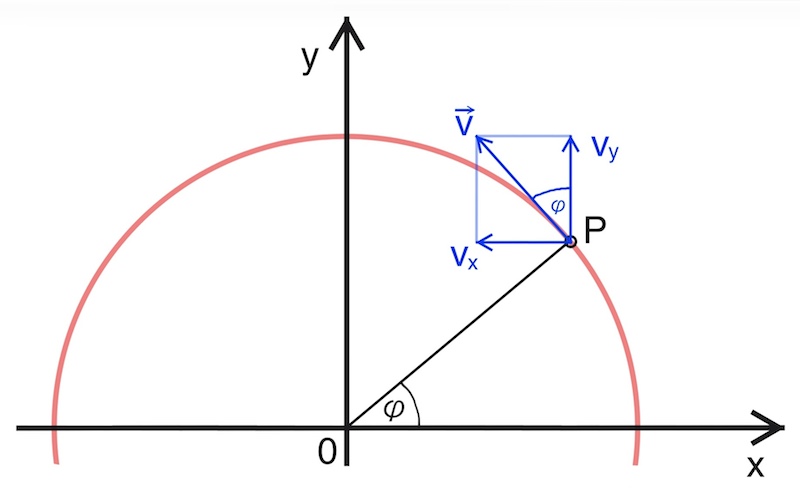
Um die Geschwindigkeit für einen bestimmten Ort bzw. Zeitpunkt zu ermitteln, bedienen wir uns erneut dem Zusammenhang zwischen einer gleichförmigen Kreisbewegung und einer harmonischen Schwingung:
Die Bahngeschwindigkeit bei der Kreisbewegung beträgt
![]()
Aus der Skizze geht hervor, dass die Geschwindigkeit bei der Schwingung dem senkrechten Anteil der Bahngeschwindigkeit entspricht. Wir nennen sie daher vy.
Für den Zusammenhang zwischen der Bahngeschwindigkeit v und der Komponente vy gilt:
![]()
Die Geschwindigkeit vy kann maximal so groß sein wie die Bahngeschwindigkeit. Dafür muss gelten: ![]() .
.
Das ist bei einem Phasenwinkel von ![]() oder
oder ![]() der Fall, also jeweils in der Ruhelage.
der Fall, also jeweils in der Ruhelage.
Wie ändert sich die Geschwindigkeit mit der Zeit?
Für den zeitlichen Verlauf der Geschwindigkeit vy ergibt sich
![]()
Die Geschwindigkeits-Zeit-Funktion ist also eine Kosinusfunktion.
Diese ist gegenüber der Sinusfunktion, also der Funktion y(t), phasenverschoben, und zwar um den Phasenwinkel ![]() bzw. um
bzw. um ![]() .
.
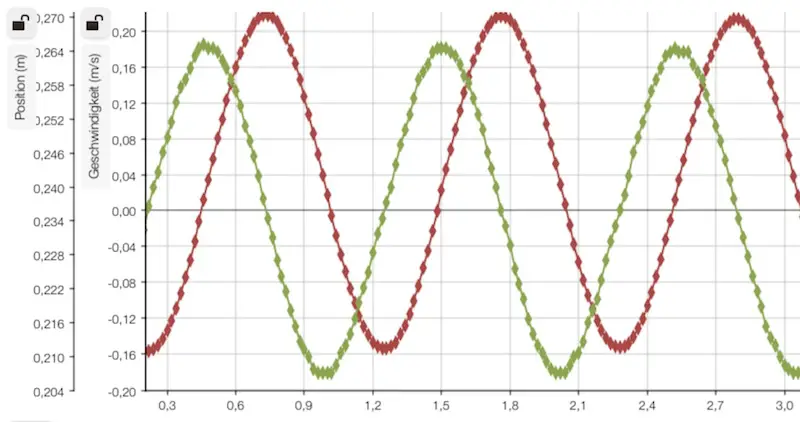
Das folgende Diagramm zeigt gleichzeitig den Verlauf der Auslenkung y (rot) sowie der Geschwindigkeit v (grün) eines Federpendels, aufgenommen mit einem Ultraschallsensor:
Der Verlauf von Auslenkung und Geschwindigkeit zeigt, dass die Geschwindigkeit jeweils bei maximaler Auslenkung (also in den Umkehrpunkten) 0 ist und ihr Vorzeichen wechselt.
Maximale Geschwindigkeit vmax
Die Geschwindigkeit erreicht ihren maximalen Wert jeweils in der Gleichgewichtslage, also bei y = 0.
Die maximale Geschwindigkeit ![]() entspricht dabei der Bahngeschwindigkeit bei der Kreisbewegung.
entspricht dabei der Bahngeschwindigkeit bei der Kreisbewegung.
Es gilt also wie für die Bahngeschwindigkeit
![]() oder anders geschrieben:
oder anders geschrieben: ![]()
Der Radius r entspricht dabei der Amplitude ymax.
Damit ergibt sich:
![]()
mit ![]() gilt also
gilt also
![]()
Damit gilt für die Geschwindigkeit eines harmonischen Oszillators in Abhängigkeit von der Zeit:
![]()
Maximale Geschwindigkeit eines harmonischen Oszillators
Wie bereits erwähnt kann der Kosinusterm ![]() maximal den Wert 1 bzw. -1 annehmen. Das ist für den Phasenwinkel
maximal den Wert 1 bzw. -1 annehmen. Das ist für den Phasenwinkel ![]() bzw.
bzw. ![]() , also immer in der Ruhelage der Fall. Dann ist v = vmax (bzw. v = -vmax).
, also immer in der Ruhelage der Fall. Dann ist v = vmax (bzw. v = -vmax).
Die maximale Geschwindigkeit lässt sich also berechnen, indem man einfach den Kosinusterm weglässt:
![]() bzw.
bzw. ![]() (s.o.)
(s.o.)