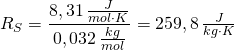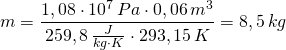Die universelle Gasgleichung

Von der allgemeinen Gasgleichung zur universellen Gasgleichung

Die Allgemeine Gasgleichung lautet: $\dfrac {p\cdot V}{T}=konst.$

Dabei ist der Wert für die Konstante auf der rechten Seite nicht beziffert.

Doch wovon hängt diese Konstante ab?

Vorüberlegung:

Bei gleichem Druck und gleicher Temperatur ist das Volumen eines Stoffs umso größer, je größer die Stoffmenge bzw. die Anzahl der Teilchen (Atome oder Moleküle) ist.

Offensichtlich gilt:

Die doppelte Gasmenge (also die doppelte Teilchenzahl) nimmt bei gleichen äußeren Bedingungen das doppelte Volumen ein. Das Volumen ist bei gleichem Druck und gleicher Temperatur also proportional zur Teilchenzahl N.

Es muss also gelten:

$\dfrac {p\cdot V}{T}\sim N$ (mit N = Teilchenzahl)

Um daraus eine Gleichung zu machen, benötigen wir einen Proportionalitätsfaktor, den wir k nennen.

Damit gibt sich:

$\dfrac {p\cdot V}{T}=k\cdot N$ oder umgeformt $p\cdot V=N\cdot k\cdot T$

Diese Gleichung wird als thermische Zustandsgleichung idealer Gase oder auch universelle Gasgleichung bezeichnet.

Die Konstante k ist dabei die Boltzmann-Konstante. Man erhält sie, wenn die Zustandsgrößen und die Teilchenzahl eines Gases bekannt sind und man diese Werte in die nach k umgestellte Gleichung einsetzt:

$k=\dfrac {p\cdot V}{N\cdot T}$

Die Einheit der Boltzmann-Konstanten ergibt sich aus den Einheiten der verknüpften Größen:

$\dfrac {Pa\cdot m^{3}}{K}=\dfrac {Nm^{3}}{m^{2}K}=\dfrac {J}{K}$

(Es gilt: $1\,Pa=1\,\frac {N}{m^{2}}$ und $1\,Nm=1\,J$ )

Der Literaturwert der Boltzmann-Konstanten beträgt

$k=1,38\cdot 10^{-23}\frac {J}{K}$

Wie man die Boltzmann-Konstante aus bekannten Zusammenhängen berechnen kann, erfährst Du weiter unten.

Universelle Gasgleichung

Die universelle Gasgleichung beinhaltet den Zusammenhang zwischen den Zustandsgrößen eines Gases und der Teilchenzahl:

$p\cdot V=N\cdot k\cdot T$

mit $k=1,38\cdot 10^{-23}\, \frac {J}{K}$ (Boltzmann-Konstante)

Aus der Zustandsgleichung idealer Gase folgt das

Gesetz von Avogadro:

Die Teilchenzahl N ist bei gleichem Volumen und gleichen äußeren Bedingungen (Druck, Temperatur) für alle (idealen) Gase gleich.

Stoffmenge und Teilchenzahl

Die Stoffmenge n ist eine der sieben Basisgrößen und hat die Einheit Mol.

Das Mol:

Ein System hat die Stoffmenge n = 1 mol, wenn es ebenso viele Teilchen enthält wie Atome in 12 g des Kohlenstoffisotops ¹²C enthalten sind.

Das entspricht einer Anzahl von 6,022 · 10²³ Teilchen. Diese Zahl nennt man Avogadrozahl oder Avogadro-Konstante N_A:

Avogadrozahl $N_{A}=6,0221418\cdot 10^{23}\,mol^{-1}$ *

(manchmal auch angegeben als $N_{A}=6,0221418\cdot 10^{26}\,kmol^{-1}$ )

Die Stoffmenge n lässt sich aus der Teilchenzahl N und der Avogadrozahl berechnen:

Es gilt: $n=\dfrac {N}{N_{A}}$

*Hinweis: Die Einheit $mol^{-1}$ lässt sich auch schreiben als $\dfrac {1}{mol}$ und bedeutet Teilchenzahl pro Mol. Diese beträgt 6,022 · 10²³.

Das Molvolumen

Unter dem Molvolumen V_m versteht man das Volumen, welches 1mol eines Stoffes unter Normalbedingungen einnimmt.

Die Normalbedingungen oder Standardbedingungen (STB) für Temperatur und Druck sind:

$T=273,15\,K$ (das entspricht 0°C)

$p=1\,013,25\,hPa=101\,325\,Pa$

Man erhält das Molvolumen aus dem Quotienten aus Volumen V und Stoffmenge n:

$V_{m}=\dfrac {V}{n}$

Alle (idealen) Gase haben das gleiche Molvolumen

Das Molvolumen unter Normalbedingungen (s.o.) ist für alle (idealen) Gase gleich und beträgt

$V_{m}=22,414\,\frac {l}{mol}$ bzw. $V_{m}=22,414\,\frac {m^{3}}{kmol}$

Berechnung der Boltzmann-Konstanten

Auch ohne Messungen lässt sich mit Hilfe der beschriebenen Zusammenhänge die Boltzmann-Konstante berechnen:

Wir setzen in die universelle Gasgleichung

$p\cdot V=N\cdot k\cdot T$

für den Druck und die Temperatur die Werte für Normalbedingungen ein, also

T = 273,15 K und p = 101325 Pa.

Wir wissen nun, dass das Volumen für die Teilchenzahl N = N_A bei Normalbedingungen dem Molvolumen von V_m = 22,414 l ≈ 0,0224 m³ entspricht.

Setzt man diese Werte in die nach k umgeformte Zustandsgleichung (s.o.) ein, so erhält man für die Boltzmann-Konstante den o.g. Wert:

$k=\dfrac {p\cdot V}{N\cdot T}=\dfrac {101\,315\,Pa\cdot 0,0224\,m^{3}}{6,022\cdot 10^{23}\cdot 273,15\,K}=1,38\cdot 10^{-23}\, \frac {J}{K}$

Die universelle Gaskonstante

Wir wollen nun in die universelle Gasgleichung anstelle der Teilchenzahl N die Stoffmenge n einsetzen.

Mit $n=\dfrac {N}{N_{A}}$ (s.o.) gilt für die Teilchenzahl: $N=n\cdot N_{A}$ .

So lässt sich die universelle Gasgleichung schreiben als

$p\cdot V=n\cdot N_{A}\cdot k\cdot T$ .

Sowohl die Avogadrozahl als auch die Boltzmann-Konstante sind Konstanten. Ihr Produkt ist also ebenfalls eine Konstante.

Das Produkt aus Avogadrozahl und Boltzmann-Konstante heißt

Universelle Gaskonstante R: $R=N_{A}\cdot k=8,3145\, \frac {J}{mol\cdot K}$

Setzt man die universelle Gaskonstante in die Zustandsgleichung ein, so erhält man die universelle Gasgleichung in folgender Form:

Universelle Gasgleichung

$p\cdot V=n\cdot R\cdot T$

mit $R=8,3145\,\frac {J}{mol\cdot K}$ (universelle Gaskonstante)

Zusammenhang zwischen Stoffmenge und Masse

Häufig wird anstelle der Stoffmenge n mit der Masse m gerechnet.

Frage: Wie kann man aus der Masse einer bestimmten Gasmenge auf die Stoffmenge bzw. die Teilchenzahl schließen?

Berechnung der Atommasse

Wir berechnen aus der Definition des Mols (s.o.) zunächst die Masse eines ¹²C-Atoms:

Es gilt:

1mol ¹²C, also 6,022 · 10²³ ¹²C-Atome, haben eine Masse von 12 g.

Die Masse eines Mols eines Stoffs bezeichnet man als molare Masse oder Molmasse M.

Um die Masse eines ¹²C-Atoms zu berechnen, muss man also die Masse eines Mols ¹²C durch die Avogadrozahl teilen:

$m\left( ^{12}C\right)=\dfrac {12\,g}{6,022\cdot 10^{23}}=1,993\cdot 10^{-26}\,kg$

Die Zahl “12” vor dem chemischen Symbol C ist die sogenannte Massenzahl. Sie ist gleich der Anzahl der Kernbausteine eins Atoms (Protonen und Neutronen) und wird auch als relative Atommasse A_r bezeichnet.

1/12 der Masse des ¹²C-Atoms (also eine relative Atommasse von A_r = 1) entspricht der atomaren Masseneinheit in der Einheit u:

Atomare Masseneinheit: 1 u = 1,6605 · 10^-27kg

Für das ¹²C-Atom gilt also:

Die relative Atommasse ist 12, die absolute Atommasse beträgt 12 u = 1,993 · 10^-26kg, und die Masse eines Mols beträgt 12 g.

Die molare Masse M (s.o.) hat die Einheit $\dfrac {g}{mol}$ und hat den gleichen Zahlenwert wie die relative Atommasse bzw. die Massenzahl.

Die molare Masse von ¹²C beträgt also $M=12\,\frac {g}{mol}$ .

Anderes Beispiel:

Sauerstoff hat das chemische Symbol O. Die Massenzahl ist 16, man schreibt also ¹⁶O.

Damit ist auch die relative Atommasse 16, die molare Masse beträgt also $M=16\, \frac {g}{mol}$ .

Mit Hilfe der molaren Masse lässt sich ein Zusammenhang zwischen der Stoffmenge und der Masse herstellen.

Es gilt: $n=\dfrac {N}{N_{A}}=\dfrac {m}{M}$

Dazu ein einfaches Beispiel:

24 g Kohlenstoff ¹²C enthalten 2 · N_A Teilchen, die Stoffmenge beträgt also 2 mol.

Damit gilt:

$\dfrac {m}{M}=\dfrac {24\,g}{12\,g}=2$

Da verschiedene Gasatome bzw. -moleküle unterschiedliche Massen haben, hat die Anzahl der Teilchen bzw. die Stoffmenge pro kg, also der Quotient $\dfrac {n}{m}$ , für jedes Gas einen spezifischen Wert.

Multipliziert man diesen Wert mit der universellen Gaskonstanten R, so erhält man die

spezifische Gaskonstante R_S: $R_{S}=\dfrac {n}{m}\cdot R$

Die Einheit der spezifischen Gaskonstanten lautet $\dfrac {J}{K\cdot kg}$ .

Damit lässt sich die Zustandsgleichung idealer Gase schreiben als

$p\cdot V=m\cdot R_{S}\cdot T$

Die spezifische Gaskonstante lässt sich für jedes Gas nachschlagen. Sie lässt sich aber auch aus der molaren Masse (bzw. aus der Massenzahl der Gasatome) und der universellen Gaskonstanten berechnen.

Eine Beispielrechnung dazu findest Du in der folgenden Aufgabe.

Beispielaufgabe zur universellen Gasgleichung

Eine 60l-Gasflasche ist mit Sauerstoff gefüllt. Bei einer Temperatur von 20°C beträgt der Druck in der Gasflasche 10,8 MPa.

Aufgabe: Berechne die Masse des in der Gasflasche enthaltenden Sauerstoffs!

Vorüberlegung:

Bei den genannten Bedingungen kann Sauerstoff annähernd als ideales Gas betrachtet werden. Es kann also die universelle Gasgleichung zur Anwendung kommen.

Die zur Berechnung erforderliche spezifische Gaskonstante von Sauerstoff kann in einem Tabellenwerk nachgeschlagen werden.

Man erhält den Wert $R_{S}=259,8\,\frac {J}{K\cdot kg}$