Wärmeenergie quantitativ

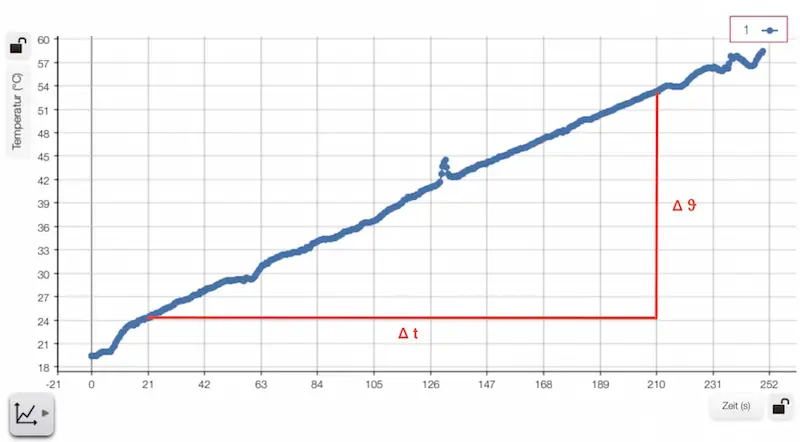
Messung der Wärmeenergie

Die einem Körper oder einem Stoff zugeführte Wärmeenergie Q soll nun qualitativ erfasst werden.

Führt man einem Körper Energie in Form von Wärme zu, ohne dass sich sein Aggregatzustand ändert, so erhöht sich seine Temperatur.

Frage:

Wie kann man aus der Temperaturänderung eines Körpers auf die zugeführte Wärme schließen?

Die Energie, die man braucht, um einen Körper bzw. einen Stoff zu erwärmen, hängt ab

• von der Temperaturerhöhung
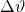
• von der Stoffmenge 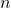bzw. der Masse 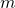des erwärmten Stoffs
• von der Art des Stoffs (Material)

Bestimmung der benötigten Energie zur Erwärmung von Wasser

Die Abgabe einer definierten Energiemenge an einen Stoff ermöglicht ein Tauchsieder in Wasser. Die vom Tauchsieder abgegebene Energie wird vom Wasser praktisch vollständig aufgenommen.

Vorüberlegungen:

1) Wie ermittelt man die vom Tauchsieder abgegebene Energie E?

Auf dem verwendeten Tauchsieder findet man die Angabe der Leistung P. Sie beträgt in unserem Fall P = 300 W (Watt).

Das bedeutet, der Tauchsieder gibt pro Sekunde eine Energie von E = 300 J (Joule) an das Wasser ab, denn es gilt:

  bzw.      und damit  

und damit für die Einheiten

  bzw.  

Die vom Wasser aufgenommene Wärme Q entspricht der vom Tauchsieder abgegebenen Energie E.

Um diese zu ermitteln, braucht man also nur die Zeitspanne  der Erwärmung zu messen.

2) Zusammenhang zwischen aufgenommener Wärme Q und Wassermenge

Erwärmt man verschiedene Wassermengen mit dem gleichen Tauchsieder, so dauert es umso länger, eine bestimmte Temperaturerhöhung   bzw.  zu erreichen, je größer die Wassermenge ist.

Für die doppelte Wassermenge wird die doppelte Zeit und damit die doppelte Energie benötigt.

(Gedankenexperiment: Erhitzt man nacheinander zweimal die gleiche Wassermenge um den gleichen Temperaturbetrag, so wird dies jeweils gleich lange dauern. Insgesamt benötigt man also die doppelte Zeit und damit die doppelte Energie.) 

Es gilt also:

Die benötigte Energie E und damit die ausgetauschte Wärme Q ist proportional zur Masse m des erwärmten Wassers:

Außerdem dauert die Erwärmung natürlich umso länger, je größer die Temperaturdifferenz ist, also je heißer das Wasser werden soll.

Der Zusammenhang zwischen Temperaturdifferenz und benötigter Wärme soll mit dem nachfolgenden Versuch ermittelt werden:

Versuch:

Das Wasser in eine Becherglas wird mit dem Tauchsieder erhitzt. Dabei wird mit Hilfe eines Temperatursensors die Temperatur gemessen und die Temperaturänderung über einen bestimmten Zeitraum erfasst.

Damit sich die aufgenommene Wärme gleichmäßig im Wasser verteilt, wird dabei ständig gerührt.

Aus der Zeit lässt sich die abgegebene (Wärme-) Energie berechnen, denn es gilt (s.o.):

Messwerte:

Es werden 400ml Wasser in das Becherglas gefüllt.

Die Masse des Wassers beträgt damit

m = 400g

Der Temperaturverlauf wird mit Hilfe eines Temperatursensors und entsprechender Software aufgezeichnet:

Ergebnis:

Aus dem Diagramm lässt sich erkennen, dass die Temperatur weitgehend linear ansteigt.

Damit gilt:    

Da die Zeitspanne proportional zur aufgenommenen Wärme Q ist (s.o. – es gilt ), ergibt sich aus dem Diagramm, dass auch Temperaturänderung und aufgenommene Wärmemenge Q zueinander proportional sind:

Zusammen mit der Proportionalität zwischen Wärmeenergie Q und Masse m (s.o.) ergibt sich:

Das bedeutet, dass der Quotient beider Seiten konstant ist:

Diese Konstante gibt an, welche Wärmemenge Q erforderlich ist, um eine bestimmte Menge eines Stoffs um eine bestimmte Temperaturdifferenz zu erwärmen. Sie hängt nur vom Material ab, ist also stoffspezifisch, und heißt spezifische Wärmekapazität c.

Beim Abkühlen wird bei gleicher Temperaturdifferenz die gleiche Wärmemenge wieder abgegeben.

Bestimmung der spezifischen Wärmekapazität von Wasser

Mit Hilfe des aufgezeichneten Temperaturverlaufs soll nun die spezifische Wärmekapazität von Wasser bestimmt werden.

Dazu benötigen wir die Temperaturänderung , die aufgenommene Wärme Q sowie die Masse m des erwärmten Wassers.

Im Diagramm ist für eine bestimmte Zeitspanne die Temperaturänderung  als Steigungsdreieck eingezeichnet. Liest man die Werte ab, so erhält man:

und

Die Wärme Q ergibt sich aus der benötigten Zeit :

Nun setzen wir alle Werte in die Gleichung für die spezifische Wärmekapazität ein und erhalten

Zum Vergleich: Der Literaturwert beträgt

Fehlerquellen:

Die Hauptfehlerquelle ist, dass ein Teil der zugeführten Energie an die Umgebung abgegeben wurde. Aus diesem Grund wurde mehr Energie benötigt, weshalb der ermittelte Wert zu groß ist.

Da die Ursache für diesen Fehler im Versuchsaufbau begründet ist und nichts mit Messungenauigkeiten zu tun hat, spricht man von einem systematischen Fehler.

Weitere mögliche Fehlerquellen sind:

• Ungenaue Bestimmung der Steigung im Diagramm
• Der Tauchsieder gibt nicht genau 300 J pro Sekunde ab
• Es wurde nicht genügend umgerührt

Grundgleichung der Wärmelehre

Kennt man die spezifische Wärmekapazität eines Stoffs, so lässt sich damit die Wärmemenge berechnen, die man braucht, um eine bestimmte Masse dieses Stoffs um 1 K zu erwärmen.

Der Zusammenhang zwischen Temperaturänderung, zu- oder abgeführter Wärme, Masse sowie spezifischer Wärmekapazität wird mit der sog. Grundgleichung der Wärmelehre erfasst, die sich aus der einfachen Umstellung der Gleichung für die spezifische Wärmekapazität ergibt:

      bzw.     

Beispielaufgabe:

Welche Wärme Q ist erforderlich, um einen Liter Wasser von 20° C auf 85° C zu erwärmen?

Lösung:

Die Masse des Wassers ergibt sich aus der Dichte und dem Volumen. 1 l Wasser hat eine Masse von 1 kg.

Die Temperaturdifferenz beträgt ΔT = 85° C – 20° C = 65 K.

Die gesuchte Wärme kann mit der Grundgleichung der Wärmelehre berechnet werden:

(Da wir hier die Masse in kg eingesetzt haben, erhält man die Wärme in der Einheit kJ.)

Ergebnis:  Man benötigt eine Wärme von Q = 272,35 kJ.