Aufbau und Energie der Kerne - die Bindungsenergie

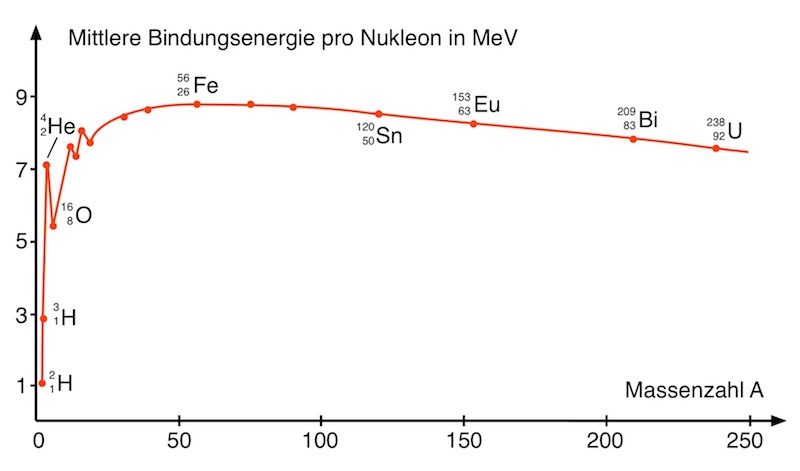
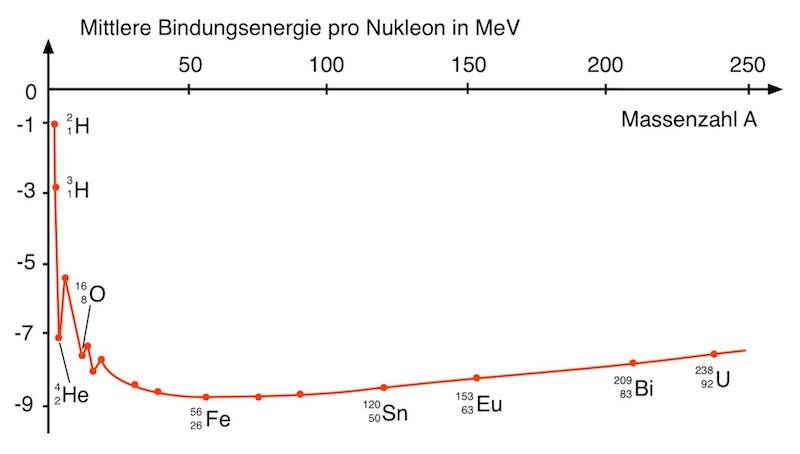
Warum halten Atomkerne zusammen?

Atomkerne bestehen aus Protonen und Neutronen, die einen extrem geringen Abstand voneinander haben. Doch warum halten Atomkerne überhaupt zusammen? Ohne weitere Kraft müssten sich die Protonen aufgrund der abstoßenden Coulombkraft mit hoher Geschwindigkeit voneinander entfernen.

Der mehr oder weniger stabile Zusammenhalt der Atomkerne legt nahe, dass es eine zwischen den Nukleonen wirkende anziehende Kraft geben muss, die stärker ist als die zwischen Protonen wirkende abstoßende Coulombkraft.

Der Massendefekt

Jedes Atom besteht aus einer bestimmten Anzahl von Protonen, Neutronen und Elektronen. Aus Kernladungszahl und Massenzahl sollte sich die Masse eines Atoms bzw. eines Atomkernes bei bekannten Massen der Bestandteile genau berechnen lassen. Wir wollen dies am Beispiel des Heliumatoms ⁴He überprüfen:

Die Masse von Atomen lässt sich experimentell sehr genau mit Hilfe von Massenspektrometern bestimmen.

Die Masse eines Heliumatoms (⁴He) beträgt $m_{A}=4,002604u$ .

Das Heliumatom besteht aus je 2 Protonen, 2 Neutronen und 2 Elektronen.

Die genauen Massen der Bausteine eines Atoms betragen in der Einheit u:

$m_{P}=1,007276467\,u$

$m_{n}=1,008664916\,u$

$m_{e}=0,000548580\,u$

Berechnet man mit Hilfe dieser Werte die Masse der Bestandteile des Heliumatoms, so erhält man

$2m_{p} + 2m_{n}+2m_{e}=4,032980\,u$

Vergleicht man nun diese Masse mit der Atommasse des Heliumatoms (s.o.), so stellt man fest:

Die Masse des Atoms ist geringer als die Summe der Massen der Bestandteile.

Die Differenz der beiden Massen beträgt $\Delta m=0,030376\,u$ .

Die gleiche Differenz ergibt sich, wenn man die Masse des Atomkerns mit der Summe der Massen der Nukleonen vergleicht.

Dieser Umstand ist nicht auf das Heliumatom beschränkt, sondern gilt für jedes Atom. Die Massendifferenz wird als Massendefekt bezeichnet.

Der Massendefekt

Die Masse eines Atomkerns ist stets kleiner als die Summe der Massen der Nukleonen.

Scheinbar geht ein Teil der Masse verloren, wenn man den Atomkern aus seinen Bestandteilen zusammensetzt. Die Massendifferenz $\Delta m$ heißt Massendefekt.

Der Massendefekt $\Delta m$ ergibt sich aus der Differenz zwischen der Summe der Massen seiner Bestandteile (Z Protonen und N Neutronen) und der Kernmasse $m_{K}$ :

$\Delta m=Z\cdot m_{P}+N\cdot m_{n}-m_{K}$

Die Neutronenzahl N erhält man aus der Differenz zwischen Massenzahl A und Kernladungszahl Z: $N=A-Z$

Die Masse des Atomkerns $m_{K}$ kann näherungsweise aus der Differenz der Masse des neutralen Atoms und der Masse der Hüllenelektronen (die Anzahl der Elektronen ist gleich der Kernladungszahl Z) berechnet werden:

$m_{K}=m_{A}-Z\cdot m_{e}$

Es gibt allerdings auch einen kleinen Massendefekt bezüglich der Atomhülle, so dass die Masse des Atoms etwas geringer ist als die Summe aus Kernmasse und den Elektronenmassen. Diese Massendifferenz entspricht einer Bindungsenergie (s.u.) zwischen den Hüllenelektronen, die der Ionisierungsenergie des Atoms entspricht – für das Wasserstoffatom im Grundzustand z.B. -13,6 eV (d.h. die Energie eines H-Atoms ist um13,6 eV kleiner als die Energie des Systems aus freien Proton und Elektron in Ruhe). Dies spielt bei Berechnungen des Massendefekts des Atomkerns jedoch so gut wie keine Rolle, daher ist die oben beschriebene Berechnung ausreichend genau.

Die Bindungsenergie

Auf die Frage, wo die fehlende Masse geblieben ist, liefert Einsteins berühmte Formel die Antwort:

Gemäß der Äquivalenz zwischen Masse und Energie E = mc² entspricht die Massendifferenz $\Delta m$ einem Energiebetrag $E_{B}=\Delta mc^{2}$ , der beim Zusammenfügen der Nukleonen zum Kern frei wird.

Diese Energie $E_{B}$ heißt Bindungsenergie.

Berechnung der Bindungsenergie:

Wir wollen nun die Bindungsenergie am Beispiel des Helium-4-Atoms berechnen. Den Massendefekt haben wir bereits berechnet (s.o.). Er beträgt:

$\Delta m=0,030376\, u$

Der Massendefekt muss zunächst in die Einheit kg umgerechnet werden.

Es gilt: $1u=1,660538921\cdot 10^{-27}\, kg$

Der Massendefekt in kg beträgt somit

$\Delta m=0,030376\, u \cdot 1,660538921\cdot 10^{-27}\, kg=5,04405\cdot 10^{-29}\, kg$

Eingesetzt in Einsteins Formel ergibt sich für die Bindungsenergie

$E_{B}=5,04405\cdot 10^{-29}\, kg\cdot c^{2}=4,533\cdot 10^{-12}\, J=28,3\, MeV$

Ergebnis: Die Bindungsenergie des ⁴He-Atomkerns beträgt E_B = 28,3 MeV.

Die Bindungsenergie des Atomkerns ist etwa um Faktor 10⁶ größer als Bindungsenergien der Elektronen in Atomhülle.

Die Bindungsenergie

Die Bindungsenergie E_B eines Atomkerns ist die Energie, die beim Zusammenfügen des Kerns aus den Nukleonen frei wird.

Der gleiche Energiebetrag wäre erforderlich, um einen Kern in seine Nukleonen zu zerlegen. Diese Energie wird als Seperationsenergie bezeichnet.

Die Bindungsenergie lässt sich gemäß der Äquivalenz zwischen Masse und Energie $E=mc^{2}$ aus dem Massendefekt $\Delta m$ berechnen:

Die Bindungsenergie beträgt $E_{B}=\Delta mc^{2}$

Durch präzise Messungen der Kernmassen mit Hilfe von Massenspektrografen konnten die Massendefekte aller Atomkerne genau bestimmt werden.

So lässt sich für jeden stabilen Kern die Bindungsenergie berechnen.

Um zwischen verschiedenen Kernen vergleichen zu können, wie stark ein Nukleon an den jeweiligen Kern gebunden ist, bietet sich als Vergleichsmaß die mittlere Bindungsenergie pro Nukleon für den jeweiligen Kern an, die sich aus dem Quotienten aus der gesamten Bindungsenergie (Bindungsenergie aller Nukleonen) und der Massenzahl A ergibt:

Mittlere Bindungsenergie pro Nukleon: E_B /A

Beispiel:

Der Kern des ⁴He-Atoms besteht aus 2 Protonen und 2 Neutronen, also aus 4 Nukleonen. Die Nukleonenzahl entspricht der Massenzahl A.

Für den Kern des ⁴He-Atoms ergibt sich für die mittlere Bindungsenergie pro Nukleon ein Wert von E_B /A = 28,3 MeV / 4 = 7,07 MeV.

In der folgenden Abbildung sind die Werte für die mittlere Bindungsenergie pro Nukleon E_B /A in Abhängigkeit von der Massenzahl (Nukleonenzahl) A dargestellt:

Mittlere Bindungsenergie pro Nukleon in Abhängigkeit von der Massenzahl

Wie man im Diagramm erkennen kann, ist die Größenordnung der mittleren Bindungsenergie pro Nukleon für einen Großteil aller Nuklide mit etwa 8 MeV pro Nukleon nahezu gleich, sie schwankt jedoch bei kleinen Massenzahlen stark.

Bei $^{4}He$ zeigt sich ein besonders hoher Wert im Vergleich zu Kernen ähnlicher Nukleonenzahl.

Bei Massenzahlen von A = 60 und knapp darüber (im Bereich der Elemente Eisen, Nickel, Cobalt) erreicht die Bindungsenergie pro Nukleon ihr Maximum und wird dann bei schwereren Kernen wieder kleiner.

Neben der obigen Darstellung kann man auch die mittlere Energie eines gebundenen Nukleons über A darstellen. Ordnet man dem Zustand, in dem die Nukleonen vollständig voneinander getrennt sind, die Energie Null zu, so ist die Energie im gebundenen Zustand negativ, da beim Zusammenbau der Nukleonen Energie frei wird (s.o.) – das gebundene System besitzt eine kleinere Gesamtenergie als die Bestandteile (Vergleiche hierzu auch die Festlegung des Energie-Nullpunkts in der Atomphysik).

Eine Kernumwandlung in einen stabileren Kern mittels radioaktiver Zerfallsprozesse erfolgt nur, wenn dies energetisch möglich ist, d.h. wenn der Ausgangskern eine größere Masse besitzt als die Summe der Massen des Tochterkerns und den Zerfallsprodukten. Die der Massendifferenz entsprechende Energie wird dann frei.

Auch die Energie, die beim α-Zerfall frei wird, kann auf diese Weise berechnet werden. Sie geht zum größten Teil in kinetische Energie des α-Teilchens über.

Aus dem Diagramm lässt sich außerdem schlussfolgern:

Energie kann sowohl durch die Spaltung schwerer Kerne als auch durch Verschmelzung (Fusion) leichter Kerne freigesetzt werden. In beiden Fällen geht das System der Nukleonen in einen energetisch niedrigeren Zustand über.

weiter mit Das Tröpfchenmodell des Atomkerns

zurück