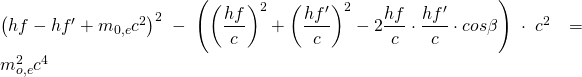Haben Photonen eine Masse?
Der sog. Compton-Effekt beruht auf der Tatsache, dass man auch Photonen eine Masse und einen Impuls zuschreiben kann.
Nach Einstein und der Formel E = mc² gilt für den Zusammenhang zwischen der Energie eines Photons E = hf und seiner trägen Masse:
![]()
Damit gilt für die Masse eines Photons
![]()
Ein Photon bewegt sich immer konstant mit der Lichtgeschwindigkeit c.
Demnach beträgt sein Impuls p (p = m·v)
![]()
Um 1922 untersuchte Arthur Holly Compton die Streuung von Röntgenstrahlen an Graphit und anderen leichten Elementen, d.h. an Elementen, bei denen die Elektronen schwach gebunden sind. Er beobachtete bei der Streuung von Röntgenstrahlen eine Wellenlängenverschiebung.
A. H. Compton erhielt 1927 für diese Entdeckung den Nobelpreis für Physik.
Während beim Fotoeffekt die gesamte Energie eines Photons von einem Elektron aufgenommen wird, gibt es Versuche, bei denen nur ein Teil der Energie von Photonen auf Elektronen übertragen wird:
Der Compton-Effekt
Bei der Streuung von Röntgenstrahlen (Röntgenphotonen haben eine wesentlich größere Energie als die Ablösearbeit beim Fotoeffekt) an quasi freien Elektronen (z.B. in Graphit) entsteht neben spektral unveränderter Streustrahlung noch eine spektral verschobene Komponente mit vergrößerter Wellenlänge abhängig vom Streuwinkel:
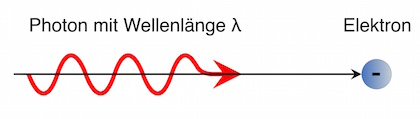 Ein Röntgenphoton mit der Wellenlänge λ trifft auf ein freies Elektron
Ein Röntgenphoton mit der Wellenlänge λ trifft auf ein freies Elektron
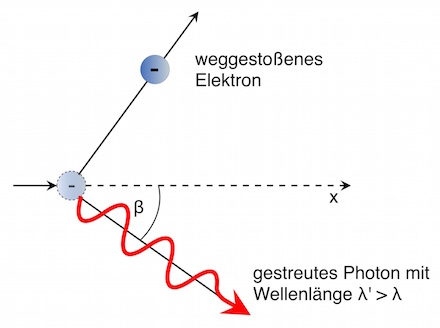
Durch den Stoß wird das Elektron weggestoßen, das Röntgenphoton wird gestreut.
Dabei vergrößert sich die Wellenlänge des Photons.
Dieser Effekt wird als Compton-Effekt bezeichnet.
Dabei hängt die Wellenlängenänderung vom Streuwinkel β ab.
Klassische Berechnungen führen zum richtigen Ergebnis
1923 gelang es Compton, diesen Effekt mit Hilfe der Vorstellung von „Lichtteilchen“ zu erklären, die wie die Kugeln beim Billardspielen auf die Elektronen nach den Stoßgesetzen des elastischen Stoßes aufeinanderprallen:
Ein Röntgenphoton mit der Energie hf prallt auf ein Elektron (mit der Masse m0) des Streumaterials, ändert dabei seine Richtung und überträgt einen Teil seiner Energie auf das Elektron.
Danach fliegt das Photon mit weniger Energie hf’ in eine andere Richtung weiter.
Compton ordnete den Photonen neben einer Energie einen Impuls zu und behandelte den Stoß zwischen Photonen und Elektronen wie den zweier Billardkugeln.
Der Photonenimpuls (s.o.) beträgt nach p = mv und der Einsteinschen Beziehung E = mc2 sowie der Photonenenergie EPhoten = hf:
![]()
Damit lässt sich dem Photon auch eine Masse zuordnen. Sie beträgt
![]()
Da sich Photonen stets mit Lichtgeschwindigkeit ausbreiten, kann man ihnen keine Ruhemasse zuordnen, sondern nur relativistische Masse und Impuls.
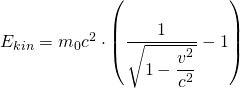
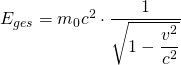 mit
mit 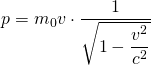
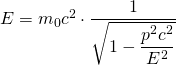 |
| 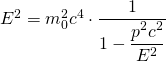 |
|