Das Potentialtopfmodell

Das Potentialtopfmodell

Wie wir inzwischen wissen, haben Mikroobjekte, wie Elektronen, Photonen, Protonen oder Neutronen Welleneigenschaften.

So, wie das Verhalten der Elektronen in der Atomhülle mit einer Wellenfunktion beschrieben werden kann, lässt sich auch das Verhalten von Nukleonen im Kern mit Wellenfunktionen beschreiben.

Analog zum Modell des linearen Potentialtopfes für die Atomhülle wird das energetische Potential im Atomkern mit dem sogenannten Potentialtopmodell beschrieben:

Der Wirkungsbereich der starken Kernkraft reicht etwa 1,5 fm (1,5 ⋅ 10^-15 m) weit. Bei größerem Abstand sinkt die Anziehungskraft schnell auf Null.

(Bei Abständen unter 0,5 fm gibt es sogar eine abstoßende Wirkung. Das erklärt die konstante Dichte von Atomkernen.)

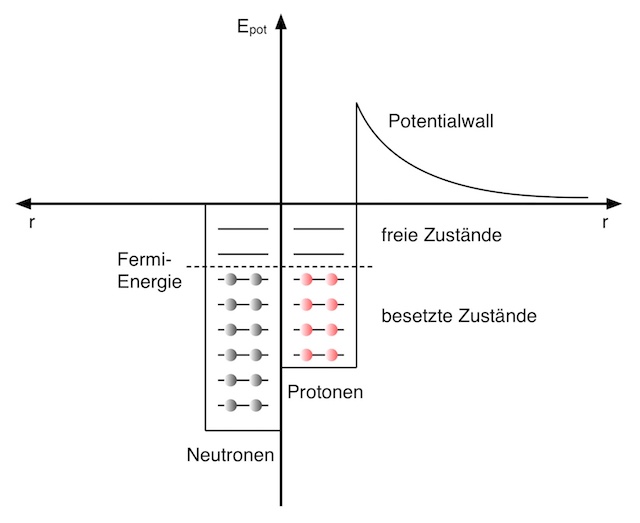
Das energetische Potential dieser Kernkraft zeigt in seinem Ortsverlauf ein kasten- oder topfförmiges Aussehen – daher die Bezeichnung Potentialtopmodell:

Für Neutronen und Protonen existieren getrennte Potentialtöpfe. Die Energieniveaus sind in beiden Töpfen bis zur Höhe des Fermi-Niveaus besetzt.

(Als Fermi-Energie wird die Energie des höchsten besetzten Zustandes bezeichnet.)

Um Kugeln aus dem Topf zu entfernen, muss man sie hochheben, also ihre potentielle Energie erhöhen. Die Nukleonen müssen die Kernkraft überwinden, um den Kern zu verlassen.

Da sich die Protonen im Kern untereinander abstoßen, ist es leichter, ein Proton aus dem Kern zu entfernen als ein Neutron. Der Potentialtopf für Protonen verschiebt sich zu höheren Energien. Der Topf ist für Neutronen daher tiefer als für Protonen.

Der Potentialwall

Nähert man dem Kern von außen ein Proton, so wird es zunächst abgestoßen. Es muss also gegen eine zunehmende abstoßende Kraft “geschoben” werden, so als müsste man es „einen Berg hinauf rollen“.

Man sagt: Es existiert ein sog. „Potentialwall“ am Rand des Protonentopfes:

Gerät das Proton in den Wirkungsbereich der Kernkräfte, gehen der Kern und das Proton eine Bindung ein, was physikalisch einen Energieverlust für das Proton darstellt; das Proton “fällt” in dessen „Potentialtopf“.

(Nur durch Zufuhr von Energie lässt sich diese Bindung wieder aufbrechen.)

Die Töpfe für Protonen und Neutronen sind für stabile Kerne immer etwa gleich hoch besetzt (Fermi-Niveau). Das erklärt, warum große Kerne immer mehr Neutronen besitzen als Protonen.

Mit dem Potentialtopmodell lässt sich der α- und β-Zerfall erklären

β-Zerfall:

Wenn z.B. der Neutronentopf höher als der Protonentopf besetzt ist, kann der Kern in einen stabileren (= energetisch niedrigeren) Zustand gelangen, indem sich ein Neutron unter Aussendung eines Elektrons in ein Proton verwandelt. Bei diesem β^–-Zerfall entsteht außerdem ein Antineutrino.

Die Energie der β-Strahlung ist kontinuierlich (mit charakteristischer Maximalenergie):

Die Energie verteilt sich beliebig auf Elektron und Antineutrino.

Wird nicht sofort der Grundzustand erreicht, so werden außerdem γ-Quanten emittiert.

Ist der Protonentopf höher besetzt als der Neutronentopf, kommt es umgekehrt zur β⁺-Strahlung unter Aussendung eines zusätzlichen Neutrinos.

Bei β-Zerfällen entstehen neue Kerne mit geringerer Energie.

α-Zerfall:

Bei der Kernumwandlung unter Aussendung eines α-Teilchens haben beide Kerne diskrete Energiezustände und damit besitzt das α-Teilchen eine bestimmte kinetische Energie.

Ein α-Teilchen besitzt eine besonders hohe Bindungsenergie (aufgrund der „magischen“ Nukleonenzahl).

Bei der Bildung eines α-Teilchens aus freien Nukleonen ist das Potential dieses Teilchens > 0 (charakteristischer Wert für jeweiligen Kern).

Der Tunneleffekt

Damit ein α-Teilchen aus dem Kern entkommen kann, benötigt es eine bestimmte Energie. Nach der klassischen Vorstellung müsste es den Potentialwall überwinden und würde dann vom Kern abgestoßen werden – dabei würde die potentielle Energie in kinetische Energie umgewandelt.

Die kinetische Energie des α-Teilchens müsste also der potentiellen Energie entsprechen, die es benötigt, um aus dem Kern entkommen zu können.

Beispiel:       Der Potentialwall ist bei  28 MeV „hoch“.

Überwindet ein α-Teilchen den Potentialwall, müsste es beim „Hinunterrollen“ eine kinetische Energie von 28 MeV erreichen.

Tatsächlich aber beträgt die kinetische Energie des α-Teilchens nur 4,2 MeV.

Das bedeutet: Die α-Teilchen können den Potentialwall nicht überquert haben. Dies ist innerhalb der klassischen Physik nicht erklärbar.

Es hat sich außerdem gezeigt, dass z.B. α-Teilchen mit einer Energie von E_Kin = 8,8 MeV nicht in den ²³⁸U-Kern eindringen können, obwohl dieser selbst nur α-Teilchen mit 4,2 MeV emittiert.

Außerhalb des Kerns ist das α-Teilchen allein den abstoßenden Coulombkräften ausgesetzt, wobei die potentielle Energie in kinetische Energie umgewandelt wird.

Für den aus dem ²³⁸U-Kern durch α-Zerfall entstandenen ²³⁴Th-Kern beträgt diese Energie 22 MeV.

Wieso besitzt das ausgesandte α-Teilchen also nur eine Energie von 4,2 MeV?

Nach klassischen Vorstellungen müsste das α-Teilchen praktisch auf halbem Weg durch den Potentialwall hindurch (durch einen Tunnel) gelangt sein.

Dieser Effekt wird daher als „Tunneleffekt“ bezeichnet. Er wurde 1928 von George Gamow quantentheoretisch erklärt und beruht auf der Tatsache, dass das Verhalten von Nukleonen sowie auch von α-Teilchen durch Wellenfunktionen beschrieben werden muss.

Wir erinnern uns:

Das Quadrat der Wellenfunktion ist proportional zur Aufenthaltswahrscheinlichkeit, ein α-Teilchen in einem bestimmten Abstand r vom Kernmittelpunkt anzutreffen.

Sind die Wände im Potentialtopf nicht unendlich hoch, so gibt es eine berechenbare von Null verschiedene Wahrscheinlichkeit, ein α-Teilchen außerhalb des Potentialwalls, also außerhalb des Kerns, anzutreffen.

Die Wahrscheinlichkeit dafür bestimmt die Halbwertszeit des Kerns – je größer die Wahrscheinlichkeit, umso häufiger verlassen α-Teilchen den Kern, und umso kleiner ist damit die Halbwertszeit.

Statistisch gesehen – und klassisch veranschaulicht – stoßen in einem ²³⁸U-Kern die α-Teilchen im Mittel 10³⁸ – mal gegen den Potentialwall, bevor es eine Durchdringung gibt. Die Wahrscheinlichkeit, dass ein α-Teilchen den Wall durchtunnelt, ist also äußerst gering.

Dass alle α-Teilchen eines Isotops die gleiche kinetische Energie besitzen, bedeutet, dass alle α-Teilchen den Potentialwall auf gleicher Höhe durchtunneln.

Ein α-Zerfall ist nur für solche Kerne möglich, deren Masse größer ist als die Summe der Massen der Zerfallsprodukte. Dies ist für natürliche Kerne mit einer Massenzahl unter 210 nicht der Fall, daher gibt es nur α-Strahler mit einer entsprechend hohen Massenzahl.