Quantenhafte Emission und Absorption

Lichtquanten und Energiestufen

Die Bedeutung der Rydberg-Formel wurde erst deutlicher, als der dänische Physiker Niels Bohr (1885-1962) im Jahre 1913 Einsteins Theorie der Lichtquanten auf das Atom anwandte:

Wenn Energieerhaltung als universelles Prinzip auch für das Atom gilt, dann muss die Emission eines Lichtquants der Energie E = hf mit einer Abnahme der inneren Energie des Atoms um den gleichen Betrag verbunden sein.

Da das Licht der Wasserstofflampe nur bestimmte Frequenzen enthält, kann demzufolge das Wasserstoffatom nur ganz bestimmte (diskrete) Energien annehmen.

Die Annahme für die innere Struktur des Wasserstoffatoms lautete demnach:

Sämtliche möglichen diskreten Energiestufen lassen sich mit der Rydberg-Formel berechnen und in einem sogenannten Energieniveauschema (auch “Termschema” genannt) darstellen:

Energieniveauschema des Wasserstoffatoms

In diesem Energieniveauschema wird klar, welche Bedeutung die Zahlen m und n in der Rydberg-Formel haben – es sind die Energiestufen, zwischen denen das Atom wechselt.

Statt den Bezeichnungen m und n ist auch die Schreibweise mit n₁ und n₂ üblich.

Damit lautet die Rydberg-Formel:     .

Die Zahlen n, die die Energiestufen charakterisieren, heißen Hauptquantenzahlen.

Der niedrigste Energiezustand (n = 1) heißt Grundzustand, die höheren Zustande heißen angeregte Zustande.

Aus dem Energieniveauschema lässt sich folgendes ablesen:

Die Energie eines Photons E = hf, das emittiert oder absorbiert wird, ist gleich der Energiedifferenz ΔE zwischen den Energieniveaus.

Beispiel:

Wechselt das Atom vom ersten angeregten Zustand (n = 2) in den Grundzustand (n = 1), so entspricht die Energiedifferenz ΔE = E₂ – E₁ = (-3,4 eV) – (-13,6 eV) = 10,2 eV. Das Atom emittiert also ein Photon mit einer Energie von 10,2 eV.

Mit E = hf bzw. f = E/h lässt sich die entsprechende Frequenz des emittierten Photons berechnen. Sie liegt im UV-Bereich.

Die Absorption eines solchen Photons führt zum Übergang von n = 1 nach n = 2 (roter Pfeil).

Die Energiedifferenzen werden für höhere Energiezustände immer kleiner. Je kleiner die Energiedifferenz bei einem Übergang ist, umso kleiner ist die Energie und damit die Frequenz des absorbierten oder emittierten Photons.

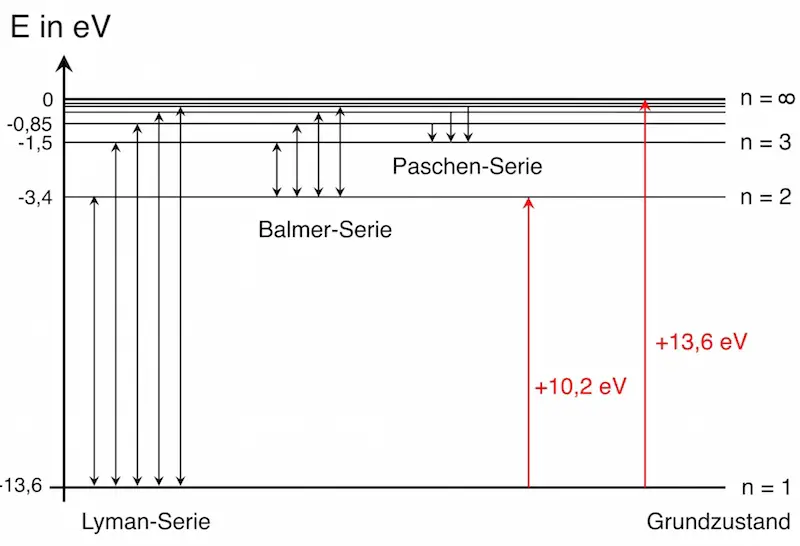
Wie sieht das in einem Atom aus?

Niels Bohr entwickelte aus seiner Vorstellung der quantenhaften Emission und Absorption ein Modell, welches an Rutherfords Kern-Hülle-Modell anknüpft, dieses jedoch mit Quantenvorstellungen verband.

Bohr ging davon aus, dass sich die Elektronen im Atom auf bestimmten kreisförmigen Bahnen um den positiv geladenen Kern bewegen:

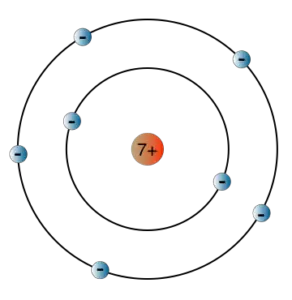
Dabei sind nur ganz bestimmte Bahnen erlaubt – denn jede Bahn entspricht einer Energiestufe.

Auch Bohr konnte allerdings nicht erklären, warum die Elektronen auf ihrer Bahn um den Kern keine Energie abgeben und dadurch in den Kern stürzen.

Er umging dieses Problem mit verschiedenen Annahmen, die als Bohr’sche Postulate bezeichnet werden. Dabei handelt es sich um letztendlich willkürliche Forderungen, die die Stabilität des Atoms erklären sollten:

1. Im Atom existieren stabile Bahnen, auf denen die Elektronen kreisen, ohne Energie abzugeben.

Außerdem postuliert er für den energetischen Aspekt eines Elektronenübergangs von einer Bahn zu einer anderen:

 2. Jede erlaubte Elektronenbahn entspricht einer bestimmten Energie E der Elektronen. Wechselt ein Elektron die Bahn, so ist die Energie des emittierten bzw. absorbierten Photons gleich der Energiedifferenz dieser Bahnen.

Es gilt:   ΔE = h · f

3. Bohr’sche Quantenbedingung

Bohr postulierte weiterhin einen Zusammenhang zwischen dem Bahnumfang U_n, der Elektronenmasse m_e, der Elektronengeschwindigkeit v_n sowie der planckschen Konstante h:

Die Bohr’sche Quantenbedingung lautet:     U_n · m_e · v_n = n · h

dabei ist n = 1, 2, 3, … (die Bahnen sind durchnummeriert, die Zahlen entsprechen den Hauptquantenzahlen)

Diese Quantenbedingung fand Bohr auf intuitivem Weg unter Verwendung einiger komplizierter Überlegungen (es gab keine zwingenden Gründe dafür).

Die Annahmen liefern richtige Ergebnisse

Trotz der scheinbar willkürlichen Annahmen konnte Bohr mit Hilfe dieser Postulate die Rydberg-Formel nicht nur herleiten sondern auch die Rydberg-Frequenz und damit sämtliche Spektrallinien des Wasserstoffatoms aus Naturkonstanten berechnen.

Das Bohr’sche Atommodell hat also eindeutige Stärken aber auch Schwächen.

Die Stärken des Bohr’schen Atommodells sind:

• Es ermöglicht die Abschätzung des Atomradius.
• Es erlaubt die Berechnung der Spektrallinien des Wasserstoffatoms.
• Es führt erste Erkenntnisse der Quantenphysik (Emission und Absorption von Lichtquanten) in die Atomtheorie ein.

Die Schwächen des Bohr’schen Atommodells sind:

• Es geht im Widerspruch zur Quantenphysik von der Existenz definierter Elektronenbahnen aus.
• Die Bohrschen Postulate erscheinen als willkürliche Annahmen.
• Bohrs Modell erlaubt für Wasserstoff richtige Vorhersagen, versagt aber bei anderen Atomen.

Wie sich mit Hilfe des Bohrschen Atommodells der Atomradius, die Energiestufen sowie die Spektrallinien des Wasserstoffatoms berechnen lassen, erfährst Du im Abschnitt “Das Bohrsche Atommodell“.