Addition von Kräften

Wenn mehrere Kräfte gleichzeitig an einem Körper angreifen, lässt sich aus den einzelnen Kräften die Gesamtkraft oder resultierende Kraft \boldsymbol {\overrightarrow {F}_{Res}} bestimmen.

Wir haben bereits einen Spezialfall dafür kennengelernt:

Wirken zwei gleich große und entgegen gerichtete Kräfte auf einen Körper, so heben sie sich in ihrer Wirkung auf. Der Körper ist im Kräftegleichgewicht, die resultierende Kraft ist Null.

Sowohl Richtung und Betrag (Zahlenwert) der resultierenden Kraft können zeichnerisch ermittelt werden. Der Betrag kann außerdem berechnet werden.

Grundsätzlich gilt:

Wenn zwei oder mehrere Kräfte gleichzeitig wirken, dann müssen die beiden Kräfte addiert werden. Doch dabei dürfen wir nicht einfach die Beträge addieren (außer die beiden Kräfte haben die gleiche Richtung)! Schließlich macht es einen Unterschied in ihrer Wirkung, in welche Richtung die Kräfte wirken.

Die Kraft ist eine vektorielle Größe

Größen, die neben einem Betrag auch eine Richtung beinhalten, nennt man vektorielle Größen. Sie werden in der Regel mit einem Pfeil über ihrem Symbol gekennzeichnet.

Diese Schreibweise wurde bereits oben bei der resultierenden Kraft verwendet: \boldsymbol {\overrightarrow {F}_{Res}}

Kräfteaddition am Beispiel

Wir wollen nun zwei Kräfte, die den gleichen Angriffspunkt haben, für verschiedene Kraftrichtungen addieren.

Wir gehen dabei immer auf die gleiche Weise vor und beginnen mit dem einfachsten Beispiel. Dann übertragen wir die Vorgehensweise auf die anderen Beispiele.

Für die Beträge der beiden Kräfte soll gelten:   F1 = 5 N     F2 = 3 N

Die beiden Kräfte werden jeweils mit Pfeilen der entsprechenden Farben dargestellt. Dabei entspricht die Länge eines Kästchens einer Kraft von 1 N.

Vorgehensweise beim zeichnerischen Addieren von zwei Kräften:

Wir hängen jeweils einen Kraftpfeil an den anderen an.

Der Pfeil der resultierenden Kraft beginnt am gemeinsamen Angriffspunkt und endet bei der Pfeilspitze des angehängten Pfeils.

Diese Vorgehensweise wollen wir nun auf verschiedene Fälle anwenden. Zusätzlich ermitteln wir den Betrag der resultierenden Kraft rechnerisch:

1. Beide Kräfte haben die gleiche Richtung

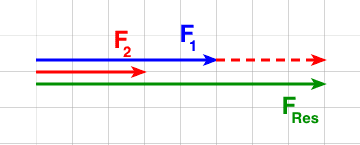
Zeichnerisch:

Hinweis: Beide Kräfte sollen den gleichen Angriffspunkt haben. Zur übersichtlicheren Darstellung sind die beiden Pfeile hier jedoch ein wenig versetzt gezeichnet. Eigentlich müssten sie exakt übereinander liegen.

Addition von Kräften gleiche Richtung

Ergebnis:

Die resultierende Kraft hat die gleiche Richtung wie die beiden Einzelkräfte. Der Betrag kann aus der Länge des Pfeils ermittelt werden. Die resultierende Kraft hat einen Betrag von FRes = 8 N.

Hinweis: Genauso hätte wir den Kraftpfeil von F1 an die Pfeilspitze von F2 anhängen können – das Resultat wäre das gleiche gewesen. Das gilt ebenso für alle nachfolgenden Beispiele.

Rechnerisch:

Für diesen Fall können wir einfach die Beträge der beiden Kräfte addieren:

F_{Res}=F_{1}+F_{2}=5\, N+3\, N=8\, N

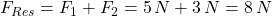
Wir erhalten das gleiche Ergebnis wie mit der zeichnerischen Methode.

2. Beide Kräfte wirken in entgegengesetzte Richtung

Zeichnerisch:

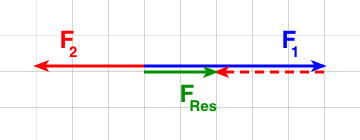
Addition von Kräften entgegengesetzte Richtung

Ergebnis:

Die resultierende Kraft ist kleiner als beide Einzelkräfte und hat die gleiche Richtung wie die größere der beiden Einzelkräfte. Die resultierende Kraft hat einen Betrag von FRes = 2 N.

Rechnerisch:

Da die beiden Kräfte entgegengerichtet sind, müssen wir einer der beiden Kräfte ein negatives Vorzeichen zuordnen.

In unserem Beispiel legen wir fest: Die Kraft F2 ist negativ und beträgt F2 = -3 N.

F_{Res}=F_{1}+F_{2}=5\, N+(-3\, N)=2\, N

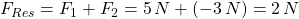
Zum gleichen Ergebnis kommt man, wenn man die Kraft F2 von F1 subtrahiert:

F_{Res}=F_{1}-F_{2}=5\, N-3\, N=2\, N

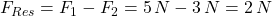
Auch hier entspricht das Ergebnis dem der zeichnerischen Methode.

3. Beide Kräfte stehen senkrecht aufeinander

Zeichnerisch:

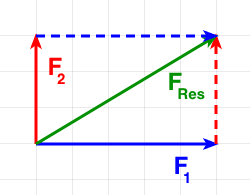
Addition von Kräften senkrecht

Ergebnis:

Die resultierende Kraft ist größer als beide Einzelkräfte (aber kleiner als die Summe der Beträge der Einzelkräfte), die Richtung liegt zwischen der der beiden Einzelkräfte.

Der Betrag der resultierenden Kraft lässt sich abmessen. Die Länge des Pfeils beträgt ca. 5,8 cm, das bedeutet, die Kraft hat einen Betrag von (ca.) FRes = 5,8 N.

Rechnerisch:

Der Pfeil der resultierenden Kraft bildet eine Diagonale zwischen den rechtwinklig zueinander stehenden Kräften F1 und F2. Diese lässt sich mit dem Satz des Pythagoras berechnen:

Es gilt: 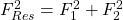  F_{Res}^{2}=F_{1}^{2}+F_{2}^{2}     und damit

F_{Res}=\sqrt {F^{2}_{1}+F^{2}_{2}}=\sqrt{(5\,N)^{2}+(3\, N)^{2}}=5,8\, N

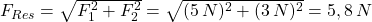
Wieder stimmt das Ergebnis mit dem der zeichnerischen Methode überein.

4. Die beiden Kräfte haben beliebige Richtungen

Zeichnerisch:

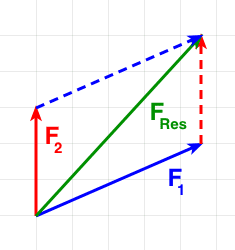
Addition von Kräften Winkel

Hinweis:

Hier müssen wir darauf achten, dass wir die Kräftepfeile jeweils exakt parallel verschieben. Führt man das mit beiden Kräften durch, so treffen sich die Pfeilspitzen der beiden Einzelkräfte in einem Punkt – es entsteht ein Parallelogramm, das sogenannte Kräfteparallelogramm.

Ergebnis:

Die Richtung der resultierenden Kraft liegt zwischen der der beiden Einzelkräfte. Je nach Richtung der Einzelkräfte ist der Betrag der resultierenden Kraft größer oder kleiner als der der Einzelkräfte.

Der Betrag der resultierenden Kraft lässt sich abmessen. Die Länge des Pfeils beträgt ca. 6,8 cm, das heißt, die Kraft hat einen Betrag von (ca.) FRes = 6,8 N.

Rechnerisch:

Die Berechnung der resultierenden Kraft ist mit den mathematischen Kenntnissen der 8. Klasse nicht möglich. Uns genügt es an dieser Stelle, die resultierende Kraft zeichnerisch zu bestimmen.

Für Interessierte:

Die Länge des Pfeils der resultierenden Kraft lässt sich mit dem sogenannten Kosinussatz berechnen. Dazu musst Du den Winkel 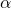\alpha zwischen den beiden Einzelkräften messen.

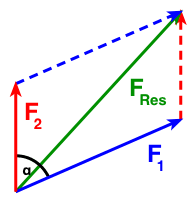Kräfteaddition WinkelDer Winkel beträgt hier etwa α = 66°.

Mit dem Kosinussatz lautet die Formel zur Berechnung der resultierenden Kraft:

F_{Res}=\sqrt{F_{1}^{2}+F_{2}^{2}+2\cdot F_{1}\cdot F_{2}\cdot cos \, \alpha}

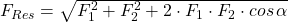
Der Kosinus (cos) dieses Winkels lässt sich mit dem Taschenrechner berechnen. Das Ergebnis lautet 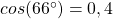cos (66^{\circ})=0,4.

Damit ergibt sich für die resultierende Kraft: 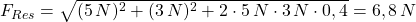    F_{Res}=\sqrt {(5\, N)^{2}+(3\, N)^{2}+2 \cdot 5\, N \cdot 3\, N \cdot 0,4}=6,8\, N

Das Ergebnis stimmt mit dem zeichnerisch ermittelten Wert überein.

Das Kräfteparallelogramm

Wenn zwei Kräfte F1 und F2 in verschiedene Richtungen gleichzeitig auf einen Körper wirken, kann ihre Wirkung durch eine resultierende Kraft (Ersatzkraft) beschrieben werden.

Die resultierende Kraft lässt sich durch Kräfteaddition zeichnerisch mit einem Kräfteparallelogramm ermitteln:

Kräfteaddition Winkel

Zerlegung von Kräften

Manchmal ist es sinnvoll, eine Kraft durch zwei einzelne Kräfte F1 und F2 zu ersetzen, die zusammen die gleiche Wirkung haben wie die ursprüngliche Kraft.

Das bedeutet: Die gegebene Kraft soll die resultierende Kraft FR aus der Addition der beiden Kräfte F1 und F2 sein.

Die beiden Kräfte F1 und F2 bezeichnet man dabei als Komponenten der gegebenen Kraft.

Kräftezerlegung an einer schiefen Ebene

Ein typisches Beispiel für eine solche Anwendung ist die Betrachtung der Kräfte an einer sog. schiefen Ebene:

Schiefe Ebene Kräfte

Ein Gegenstand befindet sich auf einer schrägen Unterlage (schiefe Ebene). Bei genügend großer Neigung rutscht (oder rollt) der Gegenstand die Schräge hinab.

Die Ursache dafür ist die Gewichtskraft des Körpers (s. Abbildung) – denn andere Kräfte wirken nicht.

Doch die Gewichtskraft hat hier zwei Wirkungen:

    1. Sie drückt den Gegenstand auf die Unterlage.
    2. Sie beschleunigt den Körper die schiefe Ebene hinab.

Entsprechend dieser beiden Wirkungen ist es sinnvoll, die Gewichtskraft in genau die Komponenten zu zerlegen, die für diese beiden Wirkungen verantwortlich sind:

Die erste Komponente können wir Anpresskraft nennen oder aber Normalkraft FN (die Kraft, die senkrecht zur Unterlage wirkt, s. Kapitel zur Reibung).

Die zweite Komponente nennen wir Hangabtriebskraft FH. Sie verläuft parallel zur Unterlage (und in Bewegungsrichtung des Körpers) und steht damit genau senkrecht zur Normalkraft.

Kräftezerlegung Schritt für Schritt

Wir haben für dieses Beispiel bereits entschieden, welche Richtungen die beiden Komponenten haben sollen. Nun müssen wir nur noch ihren Betrag ermitteln und zwar über die Länge der Kräftepfeile.

Wir haben die Gewichtskraft so eingezeichnet, dass sie in der Mitte des Körpers (im sog. Schwerpunkt) engreift.

Schritt 1:

Wir zeichnen vom gleichen Angriffspunkt aus jeweils eine dünne Linie in die Richtung der beiden gesuchten Komponenten FN und FH . Da wir noch nicht wissen, wie lang die Kräftepfeile sein werden, zeichnen wir zunächst etwas länger, als sie vermutlich sein werden:

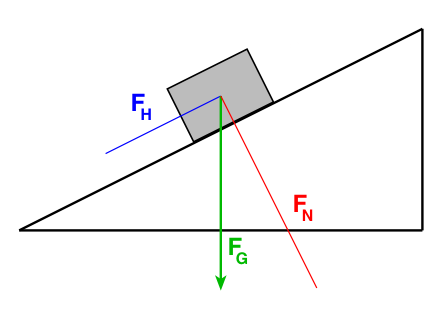Kräftezerlegung schiefe Ebene 1Nun wissen wir von der Addition von Kräften (s.o.):

Die resultierende Kraft – hier die Gewichtskraft – ergibt sich, wenn wir die Pfeile der beiden Kräfte FN und FH aneinander hängen und dabei ihre Richtung beibehalten, sie also parallel verschieben.

Schritt 2:

Wir zeichnen daher jeweils eine Parallele zu den Linien, von denen wir wissen, dass sie in Richtung der gesuchten Kräfte verlaufen, und zwar so, dass diese die Pfeilspitze der Gewichtskraft berühren und sich dort schneiden:

Kräftezerlegung schiefe Ebene 2

Schritt 3:

Nun können wir die gesuchten Komponenten einzeichnen – Sie müssen jeweils an der Spitze des Pfeils für die Gewichtskraft enden:

Kräftezerlegung schiefe Ebene 3

Die dünnen Linien könnte man anschließend entfernen. Wir erhalten wieder ein Kräfteparallelogramm (in diesem Fall ein Rechteck) und können die Länge der Pfeile messen und daraus die Beträge der Kräfte ermitteln.

Kräftezerlegung schiefe Ebene

Bei der Kräftezwerlegung an der schiefen Ebene gilt:

Je steiler die Unterlage (je größer der Winkel zwischen der schiefen Ebene und der Waagerechten), umso größer die Hangabtriebskraft und umso kleiner die Normalkraft (Anpresskraft).

Bei einem Winkel von 45° – das entspricht übrigens einer Steigung von 100% – sind beide Kräfte gleich groß.

zurück