Reibung

Reibung und Reibungskraft

Im Rahmen des Trägheitsgesetzes haben wir bereits angesprochen, dass Körper auf der Erde bei praktisch jeder Bewegung abgebremst werden – und zwar durch Reibung bzw. Reibungskräfte.

Doch was genau versteht man unter Reibung oder Reibungskraft?

Gleitreibung, Haftreibung und Rollreibung

Es gibt verschiedene Arten von Reibung, die in folgendem Beispiel erklärt werden sollen:

Wenn Du einen schweren Gegenstand, z.B. einen Schrank, verschieben möchtest, musst Du dafür eine Kraft aufwenden. Wenn Du es schaffst, den Schrank in Bewegung zu setzen, so gleitet er über den Boden. Bewegt sich der Schrank dabei gleichförmig, so benötigst Du eine Schubkraft, die genauso groß ist wie die Reibungskraft, die den Schrank abbremst (diese wirkt der Schubkraft entgegen). Der Schrank ist dann im Kräftegleichgewicht.

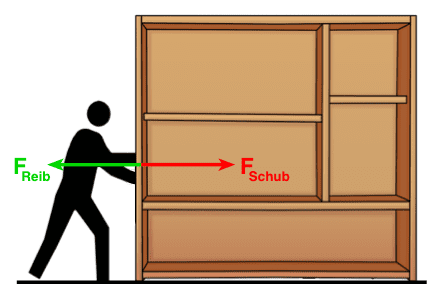
Die Reibungskraft, die den Schrank beim Gleiten über den Boden abbremst, bezeichnet man als Gleitreibungskraft F_Gleit.

Beim Anschieben wirst Du feststellen, dass Du zunächst eine etwas größere Kraft benötigst, bis der Schrank sich bewegt. Der Schrank scheint ein wenig auf dem Boden zu haften.

Diese größere Kraft, die Du zu Beginn überwinden musst, ist die sog. Haftreibungskraft F_Haft.

Möchtest Du den Schrank oder einen anderen schweren Gegenstand über eine längere Distanz verschieben, so wirst Du ihn vielleicht auf ein Rollbrett oder ein Skateboard hieven. Die beim Rollen notwendige Schubkraft ist dann deutlich kleiner, als wenn der Gegenstand über den Boden gleitet.

Man nennt die dabei zu überwindende Kraft Rollreibungskraft.

Messen der Reibungskräfte

In einem Versuch wollen wir die Reibungskräfte messen und ermitteln, von welchen Faktoren die jeweiligen Reibungskräfte abhängen. Dabei beschränken wir uns zunächst auf die Haftreibung und die Gleitreibung.

Versuch:

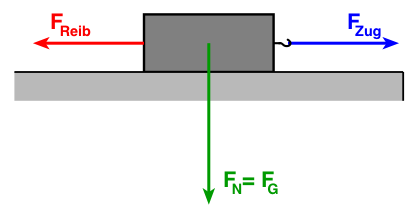
Wir legen einen Holzklotz, der auf der Unterseite mit Gummi beschichtet ist, auf einen Tisch und befestigen an einem Ende mit Hilfe eines Hakens einen Kraftmesser (s. Abbildung unten).

Dann ziehen wir langsam immer stärker am Kraftmesser parallel zur Tischplatte und beobachten die Anzeige am Kraftmesser. Die Kraft, mit der wir ziehen, bezeichnen wir als Zugkraft.

Beobachtung:

Je stärker man zieht, umso größer ist die angezeigte (Zug-) Kraft am Kraftmesser.

Zunächst bewegt sich der Klotz jedoch trotz größer werdender Zugkraft nicht – er haftet noch auf dem Tisch.

Plötzlich – bei einer bestimmten Zugkraft – setzt sich der Klotz in Bewegung. Zieht man nun gleichmäßig weiter in die gleiche Richtung, so gleitet der Körper gleichförmig über den Tisch.

Die dafür benötigte Zugkraft entspricht der Gleitreibungskraft. Diese ist kleiner als die Kraft, die wir benötigt haben, damit sich der Klotz in Bewegung setzt. Die dafür notwendige Kraft entspricht der Haftreibungskraft.

Beide Kräfte lassen sich auf diese Weise (durch Ablesen am Kraftmesser) bestimmen und notieren.

Wovon hängt die Reibungskraft ab?

Nun drehen wir den Körper um, so dass er anstatt mit der Gummiseite mit einer der Holzseiten auf dem Tisch liegt, und wiederholen den oben beschriebenen Versuch.

Ergebnis:

Wieder ist die Haftreibungskraft größer als die Gleitreibungskraft, doch beide Kräfte sind nun kleiner als im vorherigen Versuch. Die Materialien, die aufeinander reiben, scheinen also die Reibungskräfte zu beeinflussen.

Das wird Dir auch aus dem Alltag bekannt sein:

• Gummireifen oder Schuhsohlen haften besser auf einer trockenen Straße als auf einer nassen oder vereisten Straße.
  
• Ein Schlitten gleitet auf Schnee besser als auf Gras.

Außerdem wird Dir klar sein, dass es einen Unterschied macht, wie schwer der zu verschiedene Körper ist, wie groß also die Gewichtskraft des Körpers ist.

Wir wollen daher zusätzlich den Einfluss der Gewichtskraft des Körpers auf die Reibungskräfte ermitteln.

Dazu beschweren wir auf den Holzklotz mit zusätzlichen Gewichtsstücken und bestimmen jeweils die Masse bzw. die Gewichtskraft des Klotzes inkl. Gewichtsstücke. Dann wiederholen wir das Experiment und bestimmen die jeweilige Haftreibungs- und Gleitreibungskraft.

Ergebnis:

Je größer die Gewichtskraft des Körpers ist, umso größer sind auch die zu überwindenden Reibungskräfte.

Es zeigt sich ein proportionaler Zusammenhang zwischen der Gewichtskraft und den beiden Reibungskräften:

Es gilt:                und       

Zum Messen der Reibungskräfte muss also jeweils die Zugkraft gemessen werden, die erforderlich ist, um den Körper in Bewegung zu setzen (dann ist die Zugkraft gleich der Haftreibungskraft) bzw. mit konstanter Geschwindigkeit zu ziehen (dann ist die Zugkraft gleich der Gleitreibungskraft):

Reibungszahlen

Wir können den o.g. Zusammenhang daher also allgemeingültig auch mit der Normalkraft ausdrücken:

        und       

Damit gilt ebenfalls: Der Quotient aus Reibungskraft und Normalkraft ist konstant:

        sowie      

Diese Quotienten nennt man Haftreibungszahl μ_Haft (sprich: “Mü-Haft”) bzw. Gleitreibungszahl μ_Gleit (“Mü-Gleit”):

Diese Reibungszahlen sind materialspezifische Konstanten, das bedeutet, sie hängen vom Material der beiden Reibungspartner ab. Manchmal werden sie auch als Reibungskoeffizienten oder Reibwerte bezeichnet.

Berechnung der Reibungszahlen

Mit Hilfe der im oben beschriebenen Versuch ermittelten Werte für die Reibungskräfte und die Gewichtskraft (die gleich der Normalkraft ist), lassen sich die Reibungszahlen für die Reibungspartner “Gummi-Tisch” sowie “Holz-Tisch” berechnen.

Beispiel:

Der Klotz hat eine Masse von , seine Gewichtskraft beträgt damit . Diese ist gleich der Normalkraft (s.o.).

Die gemessenen Reibungskräfte betrugen

Gummi-Tisch:           

Holz-Tisch:           

Damit ergibt sich für die Reibungszahlen

Gummi-Tisch:

        

Holz-Tisch:

        

Beachte:

Die Reibungszahlen sind  – wie die Bezeichnung bereits sagt – reine Zahlen ohne Einheit. Sie geben das Verhältnis zwischen Reibungskraft und Normalkraft an.

Ist die Reibung stark, so sind die Reibungszahlen groß, bei wenig Reibung sind sie klein.

Merke: Reibungszahlen liegen in der Regel zwischen 0 und 1!

Nur bei wenigen Materialpaarungen ist die Reibungszahl größer als 1. Dann kleben die Reibungspartner förmlich zusammen.

Die Reibungszahlen hängen von vielen weiteren Faktoren ab (Temperatur, Feuchte, Oberflächenbeschaffenheit, Schmierung etc.), so dass es keine absolut richtigen Werte gibt.

Hier ein paar Richtwerte für Reibungszahlen für verschiedene Materialpaarungen:

Reibungspartner	Haftreibungszahl μHaft	Gleitreibungszahl μGleit
Stahl auf Stahl	0,2	0,1
Holz auf Stein	0,7	0,3
Holz auf Holz	0,5	0,3
Stahl auf Eis	0,03	0,01
Autoreifen auf Asphalt (trocken)	1	0,9
Autoreifen auf Asphalt (nass)	0,8	0,6
Autoreifen auf Asphalt (vereist)	0,2	0,1
Stahl auf Beton	0,35	0,2
Stein auf Stein	1	0,9

Berechnung von Reibungskräften

Sind die Reibungszahlen für eine Materialpaarung bekannt, so lassen sich Gleitreibungskraft und maximale* Haftreibungskraft berechnen:

Dazu stellen wir die Formel für die Reibungszahlen um und erhalten

Für die Haftreibungskraft:       

Für die Gleitreibungskraft:       

Beispiel:

Ein Holzkörper mit einer Masse von m = 8 kg liegt auf einer Steinoberfläche. Um ihn in Bewegung zu setzen, muss man eine Schub- oder Zugkraft aufwenden, die der maximalen Haftreibungskraft entspricht. Wir benötigen dafür die Normalkraft sowie die Reibungszahlen.

Die Normalkraft entspricht der Gewichtskraft des Holzklotzes, also

Die Haftreibungszahl für die Reibungspartner Holz auf Stein entnehmen wir der Tabelle (s.o.). Sie beträgt .

Damit können wir die maximale Haftreibungskraft berechnen:

Die Gleitreibungszahl beträgt . Damit ergibt sich für die Gleitreibungskraft

*Maximale Haftreibungskraft:

Die Haftreibungskraft kann nicht größer sein als die aufgewandte Schub- oder Zugkraft. Wollen wir wissen, bei welcher Kraft sich ein Körper in Bewegung setzt, so suchen wir die maximale Haftreibungskraft, bzw. die maximale Zugkraft.