Hookesches Gesetz

Messen von Kräften

Inzwischen kennen wir die Einheit der Kraft und kennen den Zusammenhang zwischen Masse und Gewichtskraft. Damit lassen sich Gewichtskräfte aus Masse und Orstfaktor berechnen.

Doch wie kann man andere Kräfte messen?

Wie wir wissen, können wir Kräfte an ihren Wirkungen erkennen. Wenn wir an einem Gummiband ziehen, dehnt es sich umso stärker aus, je größer die Kraft ist, mit der wir daran ziehen. Es biete sich also an, die Stärke der Verformung als Maß für die Kraft zu verwenden. Anstelle eines Gummibandes können wir auch eine Schraubenfeder aus Stahl verwenden. Auch diese verlängert sich umso stärker, je großer die Kraft ist, mit der man an ihr zieht:

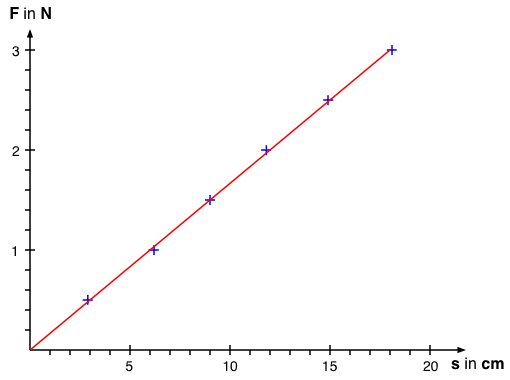
Zusammenhang zwischen Kraft und Verlängerung einer Schraubenfeder

Um den Zusammenhang zwischen der Verlängerung einer Schraubenfeder und der angreifenden Kraft zu ermitteln, bauen wir folgenden Versuch auf:

Versuch:

Wir hängen eine Schraubenfeder aus Stahl an einem Stativ auf und hängen verschiedene (bekannte) Massen an die Feder.

Wir messen jeweils die Verlängerung der Feder bei verschiedenen Massen und tragen die Messwerte anschließend in eine Tabelle (s.u.) ein.

Zusätzlich zur Masse tragen wir dort auch die jeweilige Gewichtskraft der verwendeten Massenstücke ein. Schließlich wollen wir die Verlängerung in Abhängigkeit von der angreifenden Kraft bestimmen. Die Gewichtskräfte können wir ganz einfach aus den verwendeten Massen berechnen, wie wir es im vorherigen Abschnitt bereits gelernt haben:

Es gilt: 

Da beim Messen der Verlängerung Messfehler nicht zu vermeiden sind, genügt uns bei der Berechnung der Gewichtskräft die Genauigkeit mit .

Wichtig beim Messen ist, dass wir immer jeweils die Verlängerung, also die Differenz zwischen der jeweiligen Länge und der ursprünglichen Länge (s. Abbildung), messen. Die absolute Länge der Feder spielt für uns keine Rolle.

Beispiel:

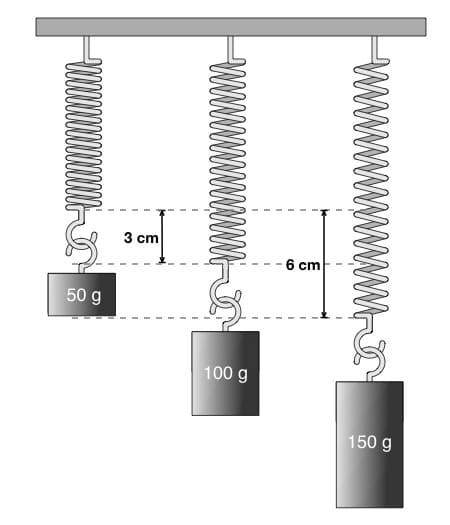
In der oberen Skizze ist zu erkennen, dass durch Anhängen einer Masse von 50 g die Verlängerung der Feder etwa 3 cm beträgt, hängt man eine Masse von 100 g an die Feder, verlängert sich diese um ca. 6 cm. Die Gewichtskraft, die auf die Feder wirkt, beträgt ca. 0,5 N bzw. 1 N.

Messwertetabelle:

Masse m in g	Gewichtskraft in N	Verlängerung in cm
50	0,5	2,9
100	1	6,2
150	1,5	9,0
200	2	11,8
250	2,5	14,9
300	3	18,1

Aus den Messwerten lässt sich vermuten: Die Verlängerung ist proportional zur angreifenden Kraft.

Um das zu überprüfen, tragen wir die Messwerte in einem Diagramm gegeneinander auf.

Ergebnis:

Die Messwerte liegen annähernd auf einer Graden. Die Abweichungen interpretieren wir als Messfehler – genauer als etwa ±2 mm lässt sich die Verlängerung sicher nicht bestimmen.

Das bedeutet, dass sich unsere Vermutung (Proportionalität zwischen Kraft und Verlängerung) bestätigt hat.

Das Hookesche Gesetz

Damit gilt also:  Kraft und Verlängerung einer Feder sind zueinander proportional:

     und damit    

In den meisten Physikbüchern findet man eine vereinfachte Schreibweise, in der man sich das Symbol für “Differenz” spart und die Verlängerung einfach mit bezeichnet wird.

Wir wollen diese Schreibweise hier übernehmen, wichtig ist aber, trotzdem daran zu denken, dass es sich bei nicht um die Länge der Feder sondern um die Verlängerung handelt.

So lässt sich vereinfacht schreiben:

     und damit    

Dieser Zusammenhang wird auch als Hookesches Gesetz bezeichnet, benannt nach dem englischen Universalgelehrten Robert Hooke (1635-1702).

Die Konstante, also der Quotient aus Kraft und Verlängerung ist umso größer, je härter die Feder ist:

Für eine härtere Feder benötigt man eine größere Kraft für die gleiche Verlängerung. Damit wird der Quotient größer.

Die Konstante wird daher auch als Federhärte oder Federkonstante D bezeichnet und hat die Einheit (“Newton pro Meter”) bzw. (“Newton pro Zentimeter”).

Kraftmesser oder Newtonmeter

Aufgrund der Proportional zwischen Kraft und Verlängerung von Schraubenfedern lassen sich diese zum Messen von Kräften verwenden, denn so kann man für eine bestimmte Feder jeder Verlängerung eine bestimmte Kraft zuordnen.

 

Ein Kraftmesser (auch Newtonmeter genannt) besteht aus einer Schraubenfeder in einer Kunststoffhülse, auf der eine Skala angebracht ist:

Je nach Größe der Kraft, die man messen möchte, verwendet man Kraftmesser mit verschieden harten Federn. Einige Kraftmesser sind so empfindlich, dass sie nur Kräfte bis 1 Newton messen können, andere dagegen lassen sich mit 20 N oder mehr belasten.

Das Bild links zeigt ein Newtonmeter, mit dem man Kräfte bis 10 N messen kann.

Im rechten Bild sieht man zwei verschiedene Newtonmeter, an denen jeweils die gleiche Masse hängt. Aufgrund der verschieden harten Federn werden diese durch die gleiche Kraft unterschiedlich stark verlängert.

Info:

Zum Messen von Kräften gibt es noch anderen Verfahren, wie z.B. Dehnungsmessstreifen (DMS) oder piezoelektrische Sensoren.

Bestimmung der Federkonstante

Mit Hilfe des Zusammenhangs, welches im Hookeschen Gesetz formuliert ist, lässt sich für jede Feder die Federkonstante bestimmen, indem man mit einer bekannten Kraft an ihr zieht und die Verlängerung misst.

Beispiel:

Die Feder in unserem Versuch verlängert sich bei einer Kraft von um ca. .

Die Federkonstante D beträgt also

Genauso hätten wir jedes andere Wertepaar einsetzen können – es kommt immer dasselbe heraus, da die Federkonstante ja eine Konstante ist.

Rechnungen mit dem Hookeschen Gesetz

Wenn man die Federkonstante einer Feder kennt, so lässt sich damit aus der Verlängerung die Kraft oder aus der angreifenden Kraft die Verlängerung berechnen:

Es gilt:          und damit          bzw.    

Beispielaufgabe:

Eine Feder mit der Federkonstante wird um 20 cm verlängert.

a) Berechne die angreifende Kraft!

Es gilt:    

Die Kraft beträgt 1 N.

b) Wie weit dehnt sich die Feder aus, wenn man mit einer Kraft von an ihr zieht?

Es gilt:    

Die Feder dehnt sich um 4 cm aus.