Der elektrische Widerstand

Wovon hängt die Stromstärke in einem Stromkreis ab?

Wir haben im letzten Abschnitt eine elektrische Spannung als Ursache für elektrischen Strom erkannt. Doch eine Spannung kann auch bestehen, ohne dass ein Strom fließt.

Die Voraussetzung für einen elektrischen Strom ist das Vorhandensein eines elektrischen Stromkreises. Ein elektrischer Stromkreis besteht neben einer Spannungsquelle aus leitenden Verbindungen und einem Verbraucher. Wenn ein Teil des Stromkreises durch einen Nichtleiter ersetzt wird, kann kein Strom fließen.

Wir haben auch bereits erkannt, dass nicht alle Stoffe den Strom gleich gut leiten. Leitungswasser ist ein schlechter Leiter, Salzwasser leitet den Strom besser, aber nicht so gut wie ein Kabel.

Die elektrische Stromstärke hängt also offenbar von der Leitfähigkeit der Bestandteile des Stromkreises ab?

Versuch:

Wir bauen einem Stromkreis auf mit einer regelbaren Spannungsquelle (also einer Spannungsquelle, bei der wir die Spannung verändern können) und einer Glühlampe als Verbraucher.

Nun messen wir bei einer bestimmten Spannung die Stromstärke. Anschließend verändern wir die Spannung und messen erneut die Stromstärke.

Ergebnis: Die Stromstärke ist umso größer, je höher die Spannung ist.

Nun ersetzen wir die Glühlampe durch einen anderen Verbraucher, z.B. durch eine Chrom-Nickel-Wendel. Dann messen wir erneut die Stromstärke bei den gleichen Spannungen wie zuvor bei der Glühlampe.

Ergebnis: Die Stromstärke unterscheidet sich trotz gleicher Spannung vom vorherigen Versuch.

Wir können daraus schließen:

Die Stromstärke in einem Stromkreis hängt ab von der angelegten Spannung und vom Verbraucher.

Verschiedene Verbraucher lassen also bei gleicher Spannung mehr oder weniger Strom fließen.

Die größte Stromstärke würde entstehen, wenn wir gar keinen Verbraucher einbauen würden. Dann hätten wir einen sog. “Kurzschluss“. Der sog. Kurzschlussstrom kann so groß werden, dass die Wärmewirkung des elektrischen Stroms die Leitungen zum Glühen bringt. Damit bei einem Kurzschluss keine Schäden auftreten, gibt es in den meisten Fällen eine Sicherung, die im Falle eines Kurzschlusses den Stromkreis unterbricht.

Da die Stromstärke durch einen Verbraucher kleiner wird, kann man sagen, dass der Verbraucher für den Strom einen Widerstand darstellt. Je stärker der Strom begrenzt wird – je kleiner also die Stromstärke ist – umso größer ist der Widerstand des Verbrauchers.

Elektrischer Widerstand

Einige Verbraucher lassen bei gleicher Spannung weniger Strom fließen als andere.

Man sagt, sie haben einen größeren Widerstand.

Der elektrische Widerstand ist ein Maß für die Behinderung des Stromflusses.

Je weniger Strom bei einer bestimmten Spannung fließt, umso größer ist der Widerstand.

Als Analogie für einen elektrischen Widerstand können wir wieder den Wasserkreislauf heranziehen:

Wenn es im Wasserschlauch eine Verengung gibt, z.B. dadurch, dass der Schlauch abgeklemmt wird oder umgeknickt ist, so kann weniger Wasser hindurchfließen. Die Engstelle stellt für das Wasser einen Widerstand dar.

Auch eine Spurverengung auf der Autobahn stellt für den Verkehrsfluss einen Widerstand dar. Der Verkehr fließt schlechter, es entsteht u.U. ein Stau.

Beim elektrischen Widerstand handelt es sich um eine genau definierte physikalische Größe. Das Formelzeichen für den elektrischen Widerstand ist ein großes “R” (aus dem Englischen: “Resistance”).

Die Definition des elektrischen Widerstandes lautet:

Der elektrische Widerstand R wird berechnet aus dem Quotienten der Spannung U und der Stromstärke I:

$R=\dfrac {U}{I}$

Die Einheit des elektrischen Widerstandes lautet Ohm (nach dem Physiker Georg Simon Ohm).

Das Formelzeichen ist ein großes Omega: Ω

Es gilt: $1\,\Omega=1\,\dfrac {V}{A}$

Berechnung des elektrischen Widerstandes

Mit der o.g. Definition können wir den elektrishen Widerstand eines Verbrauchers berechnen, wenn wir die am Verbraucher angelegte Spannung sowie die Stromstärke im Stromkreis messen.

Beispiel:

An einem Verbraucher liegt eine Spannung von U = 6 V an. Die Stromstärke, die dabei durch den Verbraucher fließt, beträgt I = 200 mA.

Mit der Formel $R=\dfrac {U}{I}$ lässt sich der Widerstand berechnen.

Wichtig dabei ist, dass wir die Stromstärke in Ampere (A), nicht in Milliampere (mA), einsetzen (also hier 0,2 A statt 200 mA).

Damit ergibt sich für den elektrischen Widerstand:

$R=\dfrac {U}{I}= \dfrac {6\,V}{0,2\,A}=30\,\Omega$

Ergebnis: Der Widerstand des Verbrauchers beträgt 30 Ω.

Wie bei allen anderen Einheiten lässt sich vor die Einheit ein Präfix setzen, wie “Kilo” oder “Mega” etc. Oft hat man es in der Praxis mit Widerstanden von einigen kΩ (Kiloohm) zu tun.

Jeder Leiter hat einen Widerstand

Letztendlich hat auch jeder Leiter sowie auch jedes Messgerät, das wir in den Stromkreis einbauen, einen Widerstand. Dabei gilt: Je besser die Leitfähigkeit, umso kleiner der Widerstand.

Anstelle des Widerstandes kann man daher auch den sog. Leitwert G angeben:

Der Leitwert

Der Leitwert G ist definiert als Kehrwert des Widerstandes R:

$G=\dfrac {1}{R}$

Die Einheit des Leitwerts heißt Siemens (S).

Ist der Widerstand groß, so ist der Leitwert klein und umgekehrt.

Je besser ein Stoff leitet, umso größer sein Leitwert und umso kleiner sein Widerstand.

Der Widerstand der leitenden Verbindungen (Kabel etc.) in einem Stromkreis ist im Vergleich zum eingebauten Verbraucher meist vernachlässigbar und beträgt einige mΩ (Milliohm).

Auch Amperemeter und Voltmeter haben einen Widerstand

Wie bereits beschrieben, hat auch jedes Messgerät einen elektrischen Widerstand. Das lässt sich nicht umgehen und muss u.U. beim Messen von Strom und Spannung berücksichtigt werden.

Widerstand eines Amperemeters – im Idealfall Null

Ein Amperemeter wird in Reihe zum Verbraucher angeschlossen. Da der Strom, der gemessen werden soll, auch durch das Amperemeter fließen muss und jeder Widerstand den Stromfluss beeinflusst, bedeutet das, dass ein Amperemeter, die Stromstärke, die wir messen wollen, verändert.

Im Idealfall dürfte ein Amperemeter also keinen Widerstand haben (es müsste also gelten: R = 0).

In der Praxis ist der Widerstand eines Amperemeters sehr klein, aber nicht null.

Solange der Widerstand des Amperemeters klein gegenüber dem Widerstand des Verbrauchers ist, so ist der Messfehler gering. Bei kleinen Widerständen im Stromkreis kann aber die Messung einen großen Fehler verursachen.

Widerstand eines Voltmeters – im Idealfall unendlich

Ein Voltmeter dagegen wird parallel zum Verbraucher eingebaut. Das bedeutet, dass wir dem Strom einen weiteren Weg – nämlich den durch das Voltmeter – zur Verfügung stellen. Das würde die Stromstärke im Stromkreis vergrößern. Außerdem wollen wir mit dem Voltmeter das “Ausgleichsbestreben elektrischer Ladungen” messen, nicht aber Ladungen fließen lassen.

Daher müsste ein Voltmeter im Idealfall einen unendlich hohen Widerstand haben (R = ∞). Da das Funktionsprinzip aber darauf beruht, dass durch den Strom ein Magnetfeld erzeugt wird, welches den Zeiger auslenkt, muss zumindest ein kleiner Strom fließen.

In der Praxis ist der Widerstand eines Voltmeters also sehr groß, aber nicht unendlich.

Solange der Widerstand des Voltmeters groß gegenüber dem Widerstand des Verbrauchers ist, so ist der Messfehler gering. Bei sehr großen Widerständen im Stromkreis kann aber die Messung einen großen Fehler verursachen.

Nun verstehst Du sicher auch, warum ein Amperemeter niemals parallel eingebaut werden darf: Dadurch würde man praktisch einen Kurzschluss erzeugen, da der Strom nahezu ungehindert durch das Amperemeter fließen könnte.

Berechnung von Stromstärke und Spannung

Ist der Widerstand in einem Stromkreis bekannt, so kann durch Messen der Spannung die Stromstärke oder durch Messen der Stromstärke die Spannung berechnet werden.

Dazu müssen wir nur die bereits verwendete Formel für den Widerstand 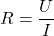$R=\dfrac {U}{I}$ entsprechend umstellen:

Für die elektrische Spannung U ergibt sich:

$U=R\cdot I$

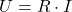
Für die elektrische Stromstärke I ergibt sich:

$I=\dfrac {U}{R}$

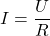
Dazu jeweils ein Beispiel:

1. Berechnung der Spannung:

Durch einen Verbraucher fließt ein Strom von I = 80 mA. Der Widerstand des Verbrauchers beträgt R = 50 Ω. Berechne die Spannung, die am Verbraucher anliegt!

Es gilt: 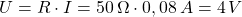$U=R\cdot I=50\,\Omega \cdot 0,08\, A=4\, V$ (wichtig: I in Ampere!)

Ergebnis: Am Verbraucher liegt eine Spannung von 4 V an.

2. Berechnung der Stromstärke:

An einem Verbraucher mit dem Widerstand R = 100 Ω liegt eine Spannung von U = 12 V an. Berechne die Stromstärke, die durch den Verbraucher fließt!

Es gilt: 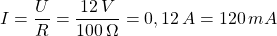$I=\dfrac {U}{R}=\dfrac {12\, V}{100\,\Omega}=0,12\, A=120\,mA$

Ergebnis: Die Stromstärke im Verbraucher beträgt 120 mA.

Widerstand als Bauteil

Als Widerstand wird neben der elektrischen Größe auch ein Bauteil in der Elektronik bezeichnet, welches u.a. genau zu dem Zweck gefertigt wird, den Strom zu begrenzen, dem Strom also einen Widerstand entgegenzusetzen.

Ein Widerstand als Bauelement besteht in der Regel aus einem isolierenden zylinderförmigen Porzellan-Körper, der mit einer dünnen Kohle- oder Metallschicht, die als Leiter dient, sowie einem Schutzlack überzogen ist. Man nennt solche Widerstände daher Kohleschicht- oder Metallschicht-Widerstände.

Widerstände sind als Bauteil sehr klein, daher ist der Widerstandswert (in Ohm) in Form von farbigen Ringen aufgedruckt, denn Zahlen könnte man in der Größe nur schwer oder gar nicht lesen. Die farbigen Ringe enthalten einen Code, aus dem man mit Hilfe einer Farbtabelle sowohl den Widerstandswert als auch die Toleranz ablesen kann.

Das Schaltzeichen eines Widerstandes sieht so ähnlich aus wie das Bauteil selbst, nämlich wie ein Zylinder mit den Leitungen an den Enden:

Schaltzeichen eines Widerstandes

zurück