Lösung der Schrödingergleichung für den linearen Potentialtopf
Nun, wo wir die Schrödingergleichung in der in Schulbüchern üblichen Schreibweise vorliegen haben, wollen wir sie für ein einfaches und bekanntes Beispiel lösen:
Die Schrödingergleichung lautet (s.o.): 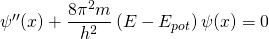
Für den linearen Potentialtopf gilt:
Innerhalb des Potentialtopfes mit der Länge 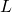 ist die potentielle Energie Null. Die Gesamtenergie ist also gleich der kinetischen Energie.
ist die potentielle Energie Null. Die Gesamtenergie ist also gleich der kinetischen Energie.
Mit 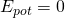 vereinfacht sich die Schrödingergleichung zu
vereinfacht sich die Schrödingergleichung zu
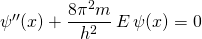 (1)
(1)
Wir kennen bereits eine mögliche Lösungsfunktion, nämlich die Wellenfunktion für stehende Wellen:
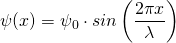
Dabei muss die Bedingung für stehende Wellen mit zwei festen Enden gelten:
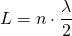 bzw.
bzw. 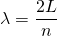
Eingesetzt in die Wellenfunktion ergibt sich
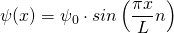
Wir benötigen auch noch die zweite Ableitung dieser Funktion. Diese lautet:
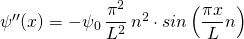
Nun setzen wir die Wellenfunktion sowie ihre zweite Ableitung in die Schrödingergleichung (1) ein:
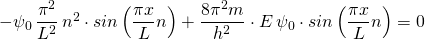
Es lässt sich 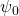 ,
, 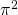 sowie der Sinusterm kürzen. Das ergibt:
sowie der Sinusterm kürzen. Das ergibt:
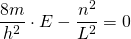 |
| 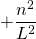 |
| 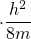
Die letzte Umformung liefert schließlich die diskreten Energiewerte im linearen Potentialtopf.
Die eingesetzte Wellenfunktion stellt also eine Lösung der Schrödingergleichung dar für die Bedingung
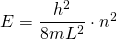
Wir erhalten also die gleichen diskreten Energien wie mit unserer Überlegung im Abschnitt Das Modell des linearen Potentialtopfes.
Berechnung von Wahrscheinlichkeiten
Nun wollen wir auch noch die Wahrscheinlichkeit berechnen, ein Elektron im linearen Potentialtopf der Länge 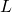 in einem bestimmten Teilbereich
in einem bestimmten Teilbereich 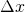 anzutreffen.
anzutreffen.
Die Wahrscheinlichkeit 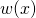 entspricht dem Produkt aus dem Quadrat der Wellenfunktion (Wahrscheinlichkeitsdichte) und einem Intervall
entspricht dem Produkt aus dem Quadrat der Wellenfunktion (Wahrscheinlichkeitsdichte) und einem Intervall 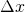 :
:
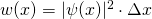
mit 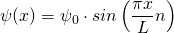 und damit
und damit 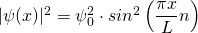
Zur Erinnerung: Es gilt: 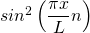

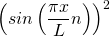
Für den Grundzustand 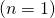 hat das Quadrat der Wellenfunktion
hat das Quadrat der Wellenfunktion 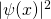 und damit die Aufenthaltswahrscheinlichkeitsdichte in Abhängigkeit vom Ort x folgende Form:
und damit die Aufenthaltswahrscheinlichkeitsdichte in Abhängigkeit vom Ort x folgende Form:
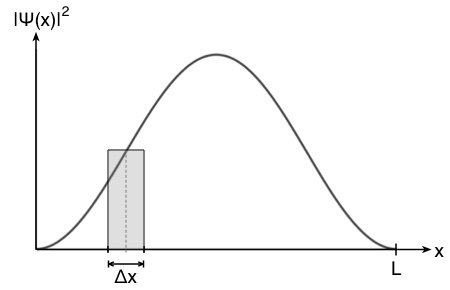
Die Aufenthaltswahrscheinlichkeitsdichte ändert sich also mit dem Ort  und damit für jedes mögliche Intervall
und damit für jedes mögliche Intervall  . Die Fläche des Rechtecks entspricht in etwa der Teilwahrscheinlichkeit des Intervalls
. Die Fläche des Rechtecks entspricht in etwa der Teilwahrscheinlichkeit des Intervalls 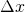 .
.
Normierung
Die Summe der Teilwahrscheinlichkeiten für alle möglichen Intervalle 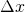 von
von 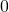 bis
bis 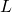 ergibt die gesamte Wahrscheinlichkeit, das Elektron im Bereich der Länge
ergibt die gesamte Wahrscheinlichkeit, das Elektron im Bereich der Länge 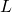 zu finden.
zu finden.
Nach der Definition des linearen Potentialtopfes (mit unendlich hohen Wänden) kann sich das Teilchen nur innerhalb der Länge 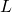 aufhalten. Die Aufenthaltswahrscheinlichkeit innerhalb des gesamten Bereichs der Länge
aufhalten. Die Aufenthaltswahrscheinlichkeit innerhalb des gesamten Bereichs der Länge 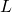 ist also 1 (oder 100%), außerhalb ist sie 0.
ist also 1 (oder 100%), außerhalb ist sie 0.
Wir müssen die Amplitude 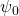 der Lösungsfunktion daher so wählen, dass diese Bedingung erfüllt wird. Das wird als Normierung bezeichnet.
der Lösungsfunktion daher so wählen, dass diese Bedingung erfüllt wird. Das wird als Normierung bezeichnet.
Teilwahrscheinlichkeiten
Um eine Teilwahrscheinlichkeit in einem Intervall 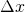 zu berechnen, muss der Funktionswert für einen Ort
zu berechnen, muss der Funktionswert für einen Ort 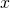 mit dem Intervall
mit dem Intervall 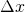 multipliziert werden.
multipliziert werden.
Da sich die Wahrscheinlichkeitsdichte innerhalb des Bereichs 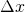 ändert, ordnen wir zur Vereinfachung dem gesamten Bereich
ändert, ordnen wir zur Vereinfachung dem gesamten Bereich 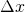 den Wert
den Wert 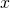 in der Mitte des Intervalls zu und tun so, als wäre der Wert über den gesamten Bereich
in der Mitte des Intervalls zu und tun so, als wäre der Wert über den gesamten Bereich 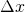 konstant.
konstant.
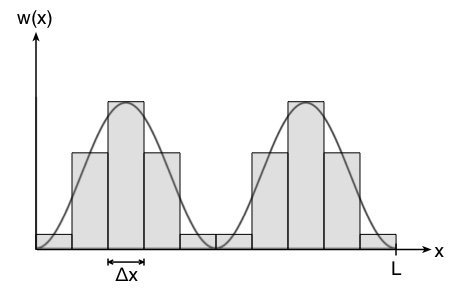
Wie man in der Abbildung oben sieht, ist der Fehler vertretbar und umso kleiner, je kleiner das Intervall 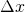 ist. Die Wahrscheinlichkeit
ist. Die Wahrscheinlichkeit 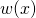 entspricht so der Fläche des Rechtecks.
entspricht so der Fläche des Rechtecks.
Für den Bereich von x = 0 bis x = L muss für die Summe aller Teilwahrscheinlichkeiten (s.o.) gelten:
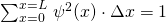 mit
mit 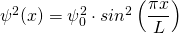 (für
(für 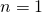 )
)
Für Intervalle 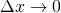 wird aus der Summe ein Integral.
wird aus der Summe ein Integral.
Die Gesamtwahrscheinlichkeit entspricht der gesamten Fläche unter der 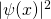 -Funktion:
-Funktion:
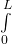
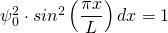 bzw.
bzw. 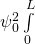
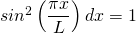
Die Lösung dieses Integrals lässt sich in einer Formelsammlung nachschlagen. Das Ergebnis ergibt den Normierungsfaktor (die Amplitude)
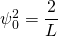 und damit
und damit 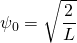
Wahrscheinlichkeiten berechnen
Mit diesem Normierungsfaktor lautet die Wellenfunktion, die eine Lösung der Schrödingergleichung darstellt
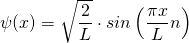 mit n = 1, 2, 3, …
mit n = 1, 2, 3, …
Damit ist
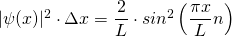 mit n = 1, 2, 3, …
mit n = 1, 2, 3, …
Die Wahrscheinlichkeit 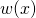 , das Elektron in einem Intervall
, das Elektron in einem Intervall 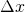 zu finden, beträgt damit
zu finden, beträgt damit
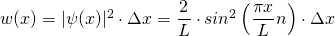 mit n = 1, 2, 3, …
mit n = 1, 2, 3, …
Für den Grundzustand (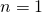 ) gilt also:
) gilt also:
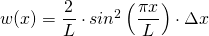
Um konkrete Werte für die Wahrscheinlichkeiten berechnen zu können, müssen wir Werte für die Länge 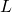 und die Intervalle
und die Intervalle 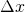 festlegen.
festlegen.
Wir wählen für 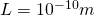 , was in etwa dem Durchmesser eines Atoms entspricht und teilen diese Länge in 10 gleich große Intervalle
, was in etwa dem Durchmesser eines Atoms entspricht und teilen diese Länge in 10 gleich große Intervalle 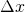 ein. Damit ist
ein. Damit ist 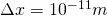 .
.
Außerdem gilt: 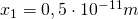 ,
, 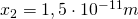 usw.
usw.
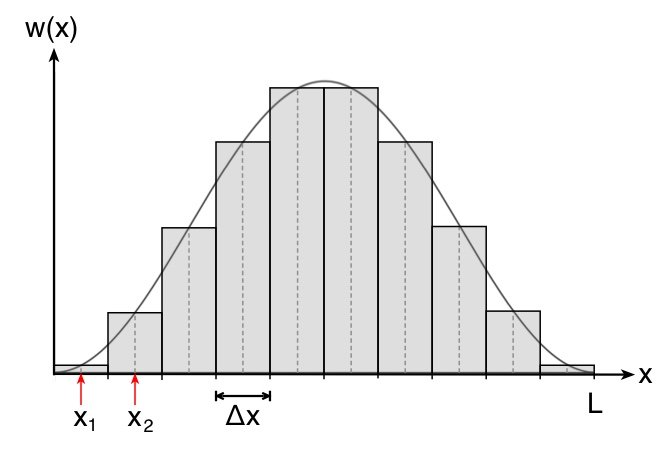
Wir tun dabei so, als ob die Wahrscheinlichkeitsdichte über den Bereich 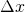 konstant sei und ordnen jedem Intervall jeweils den Mittelwert zwischen den Grenzen des Intervalls zu.
konstant sei und ordnen jedem Intervall jeweils den Mittelwert zwischen den Grenzen des Intervalls zu.
Nun lässt sich für jedes Intervall die Wahrscheinlichkeit berechnen, ein Elektron in diesem Bereich anzutreffen. Aufgrund der Symmetrie der Wahrscheinlichkeitsdichtefunktion genügt es, die Wahrscheinlichkeiten für die ersten 5 Intervalle 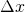 (linke Hälfte) zu berechnen – die Werte in der rechten Hälfte sind identisch.
(linke Hälfte) zu berechnen – die Werte in der rechten Hälfte sind identisch.
Berechnung der Wahrscheinlichkeit 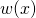 für das erste Intervall
für das erste Intervall 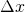 (mit
(mit 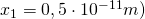 :
:
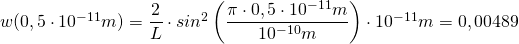
Das bedeutet, die Wahrscheinlichkeit, ein Elektron im Bereich zwischen 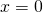 und
und 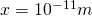 anzutreffen beträgt 0,49 %.
anzutreffen beträgt 0,49 %.
Entsprechend lassen sich die Wahrscheinlichkeiten für die anderen Intervalle berechnen. Die Ergebnisse für alle Intervalle sind in folgender Tabelle aufgeführt:

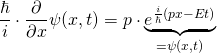
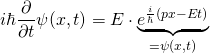
![Rendered by QuickLaTeX.com \underbrace {i\hbar\dfrac {\partial}{\partial t}}_{\widehat {E}}\psi(x,t)=\underbrace {\left[ -\dfrac {\hbar^{2}}{2m} \dfrac {\partial^{2}}{\partial x^{2}}+V(x,t) \right]}_{\widehat {H}} \psi(x,t)](http://physikunterricht-online.de/wp-content/ql-cache/quicklatex.com-0bdb610afd5217a7cc3b689edf516338_l3.png)