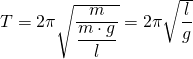Führt ein Fadenpendel eine harmonische Schwingung aus?

Ein weiteres Beispiel für eine Schwingung ist die Schwingung eines Fadenpendels: Ein an einem Faden aufgehängter Pendelkörper wird ausgelenkt und losgelassen.

Fragen:

– Welches ist die rücktreibende Kraft bei einem Fadenpendel?

– Von welchen Größen hängt die Schwingungsdauer eines Fadenpendels ab?

– Ist die Schwingung eines Fadenpendels harmonisch?

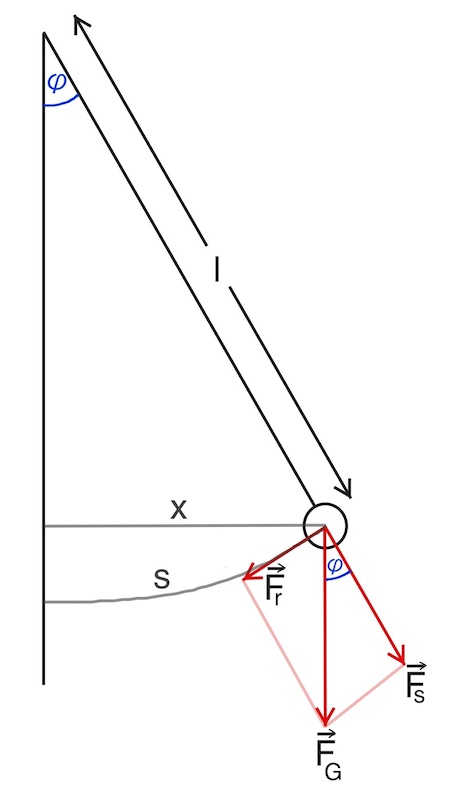
Die rücktreibende Kraft bei einem Fadenpendel muss ihre Ursache in der Gravitationskraft haben – denn andere Kräfte wirken nicht. Die Gravitationskraft ist jedoch stets nach unten gerichtet – die Rückstellkraft kann also nur einem Anteil an der Gravitationskraft entsprechen.

Wovon hängt die Schwingungsdauer ab?

Experimentell lässt sich einfach feststellen:

Die Schwingungsdauer eines Fadenpendels hängt von der Länge l des Fadens ab.

Dabei gilt: Je länger der Faden, umso größer die Schwingungsdauer

Die Schwingungsdauer hängt jedoch nicht von der Masse m des Pendelkörpers oder der Auslenkung y ab.

Ist die Schwingung eines Fadenpendels harmonisch?

Um diese Frage beantworten zu können, müssen wir untersuchen, ob das lineare Kraftgesetz gilt, also ob die Rückstellkraft proportional zur Auslenkung ist.

Dazu betrachten wir ein Fadenpendel im Punkt der maximalen Auslenkung:

Fadenpendel

Wir zerlegen die Gewichtskraft F_{G} in zwei Komponenten:

Die Komponente \overrightarrow {F}_{r}, stellt die Rückstellkraft dar. Sie muss in Bewegungsrichtung des Pendelkörpers zeigen.

Die Komponente \overrightarrow {F}_{s}, ist die Kraft, die den Faden spannt.

Ändert sich die Auslenkung, so ändert sich auch die Größe der beiden Kräfte:

Ist die Auslenkung 0 – der Pendelkörper befindet sich also in der Ruhelage – so ist die Rückstellkraft 0. Der Pendelkörper bewegt sich aufgrund seiner Trägheit über die Ruhelage hinaus und wird dann abgebremst, da die Rückstellkraft nun der Bewegungsrichtung entgegengerichtet ist.

Der Pendelkörper beschreibt bis zur Ruhelage den Weg s (Teil einer Kreisbahn).

Für kleine Auslenkungen ist dieser Weg annähenrd gleich der Strecke x.

Es gilt also:   s ≈ x

Die Rückstellkraft Fr ist abhängig von der Gewichtskraft FG und der Auslenkung.

Für die Rückstellkraft gilt:

F_{r}=sin\varphi\cdot F_{G}

Für die Gewichtskraft gilt bekanntlich:   F_{g}=m\cdot g

Damit ergibt sich für die Rückstellkraft:

F_{r}=sin\varphi\cdot m\cdot g

Aus der Skizze ergibt sich:

sin\varphi=\dfrac {x}{l}

Damit gilt für die Rückstellkraft:

F_{r}=-m \cdot \dfrac {g\cdot x}{l}

Die Rückstellkraft ist negativ, da sie der Auslenkung entgegengerichtet ist.

Für kleine Auslenkungen (s ≈ x) gilt also annähernd:

F_{r}=-m\; \dfrac {g\cdot s}{l}

Damit gilt also das lineare Kraftgesetz  F_{r}\sim s

bzw.

F_{r}=-Ds     mit     D=\dfrac {mg}{l}     (Dies ist die Richtgröße beim Fadenpendel)

Für kleine Auslenkungen ist die Bedingung für eine harmonische Schwingung also erfüllt.

Für harmonische Schwingungen haben wir bereits eine Formel zur Berechnung der Schwingungsdauer hergeleitet:

Für harmonische Schwingungen gilt:     T=2\pi\sqrt {\dfrac {m}{D}}

Setzt man für die Richtgröße D den o.g. Zusammenhang ein, erhält man für die Schwingungsdauer

T=2\pi\sqrt {\dfrac {m}{\dfrac {m\cdot g}{l}}}=2\pi\sqrt {\dfrac {l}{g}}

Ein Fadenpendel schwingt bei kleiner Amplitude harmonisch mit der Schwingungsdauer

T=2\pi\sqrt {\dfrac {l}{g}}

Die Schwingungsdauer eines Fadenpendels hängt also von der Länge des Fadens sowie der Fallbeschleunigung g ab.

Die Fallbeschleunigung bestimmt die Gewichtskraft, die auf eine bestimmte Masse wirkt und damit die Rückstellkraft.

Man kann also aus der Schwingungsdauer eines Fadenpendels auf die Fallbeschleunigung schließen.

weiter mit Gedämpfte Schwingungen
zurück