Das Modell des linearen Potentialtopfes

Der lineare Potentialtopf

Das Modell des linearen Potentialtopfes zur Beschreibung des Aufenthalts eines Elektrons scheint zunächst ein wenig abstrakt zu sein und wirft vielleicht die Frage auf, was das alles mit einem Atom zu tun haben soll. Die Bezeichnung “linearer Potentialtopf” ergibt sich letztendlich aus einer bestimmten Darstellung der potentiellen Energie, die an einen Topf erinnert.

Beschreibung des Aufenthalts eines Elektrons in einem begrenzten Bereich

Beim Modell des linearen Potentialtopfes geht es zunächst darum, einen möglichst einfachen Fall des Verhaltens eines Teilchens (z.B. eines Elektrons) zu betrachten und das Prinzip zu verstehen. Die Übertrageung auf ein Atom erfolgt zu einem späteren Zeitpunkt. Insofern ist der lineare Potentialtopf der erste Schritt zum quantenmechanischen Atommodell.

Grundüberlegung:

Die Überlegung, die zu diesem Modell führt, ist folgende:

Der Aufenthalt eines Elektrons, welches sich in einem bestimmten Bereich aufhalten kann, also quasi in diesem Bereich “eingesperrt” ist, kann durch eine stehende Welle beschrieben werden. Das Quadrat der Amplitude kann dabei als Wahrscheinlichkeit, das Elektron an einem bestimmten Ort anzutreffen, angesehen werden.

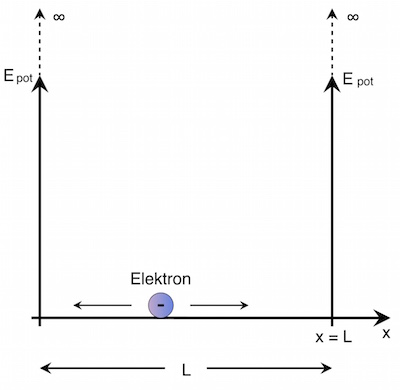
Anstelle eines (dreidimensionalen) Atoms stellt man sich nun einen eindimensionalen Bereich (also eine bestimmte Länge L) vor, in dem sich das Elektron aufhalten kann. Es soll sich in diesem Bereich kräftefrei bewegen können (wobei “bewegen” eigentlich das falsche Wort ist). Das bedeutet, es gibt keine weitere Ladung in diesem Bereich – also auch keinen Atomkern.

Wenn sich das Elektron kräftefrei “bewegen” kann, bedeutet dass, dass die potentielle Energie in diesem Bereich Null ist ( $E_{pot}=0$ ). Da es sich aber außerhalb dieses Bereiches nicht aufhalten kann, muss die potentielle Energie außerhalb dieses Bereichs unendlich groß sein.

Analogie:

Eine Kugel befindet sich in einem Topf und kann zwischen den Wänden des Topfes hin und her rollen. Damit die Kugel den Topf nicht verlassen kann, egal wie viel kinetische Energie sie besitzt, müssten die Wände des Topfes unendlich hoch sein.

Zusammenfassung:

Beim Modell des linearen Potentialtopes geht man von folgenden Vereinfachungen gegenüber einem Atom aus:

Ein Elektron ist in einem bestimmten eindimensionalen Bereich der Länge L eingesperrt.

Innerhalb dieses Bereichs ist die potentielle Energie E_pot = 0, außerhalb dieses Bereichs wird E_pot unendlich.

Damit ist die Aufenthaltswahrscheinlichkeit des Elektrons innerhalb des Bereichs 1, außerhalb dieses Bereichs ist sie 0.

Wenn E_pot innerhalb des Bereichs Null ist, kann sich das Elektron innerhalb der Länge L kräftefrei “bewegen”.

Auch wenn ein Atom natürlich dreidimensional ist und es im Atom durch den positiv geladenen Atomkern sehr wohl ein Potential gibt, lässt sich mit diesem Modell gut veranschaulichen, dass allein durch die Tatsache, dass der Aufenthaltsbereich eines Teilchens auf einen bestimmten Bereich eingeschränkt ist und der Aufenthalt des Teilchens mit einer Wellenfunktion beschrieben wird, es nur diskrete mögliche Energien gibt.

Trägt man die potentielle Energie $E_{pot}$ und den Weg $x$ gegeneinander auf, so erhält man eine Funktion mit der Form eines Topfes mit unendlich hohen Wänden:

Aus der Form der Darstellung der potentiellen Energie stammt die Bezeichnung “Potentialtopf” (s. Analogie oben).

Wellenfunktionen und Wahrscheinlichkeitenen

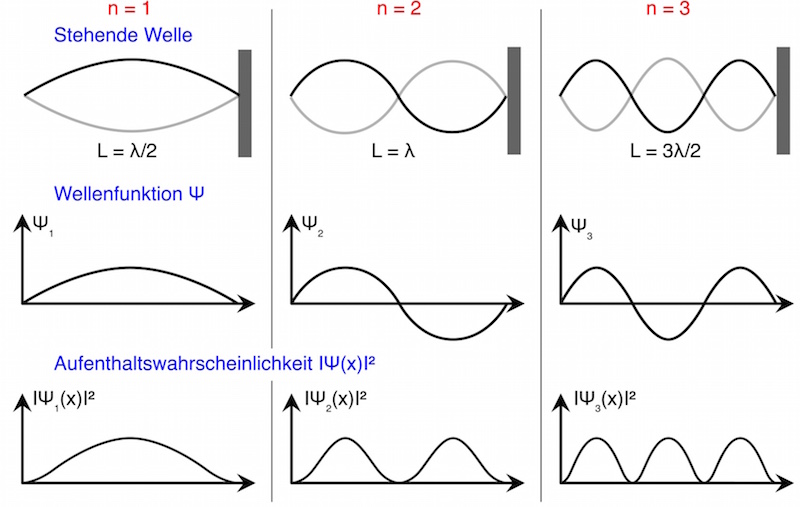
Die Wellenfunktion $\psi (x)$ , die den Aufenthalt des Elektrons beschreibt (s.o.), kann wie die einer eingespannten Feder nur bestimmte Schwingungsformen annehmen:

Die stehende Welle der eingespannten Feder entspricht bei dieser Analogie einer Wellenfunktion $\psi$ . Das Quadrat ihres Betrages $|\psi (x)|^{2}$ gibt die Wahrscheinlichkeitsdichte an, das Elektron am Ort x aufzufinden.

Das Produkt $|\psi (x)|^{2}\cdot \Delta x$ gibt die Wahrscheinlichkeit dafür an, dass sich das Elektron im Raumbereich (bzw. hier eindimensional) $\Delta x$ befindet.

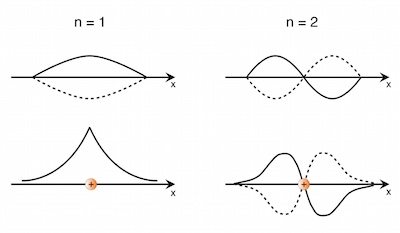
Für den Grundzustand (n = 1) erkennt man:

Die Wahrscheinlichkeitsdichte ist in der Mitte der Länge L (also bei x = L/2) am größten.

Da sich Knoten und Bäuche bei einer stehenden Welle immer am gleichen Ort befinden und sich somit der Betrag der Wellenfunktion zeitlich nicht ändert, ist die Wahrscheinlichkeitsverteilung von der Zeit unabhängig. Man spricht auch von einem stationären Zustand.

Energiewerte eines Teilchens im linearen Potentialtopf

Allgemein gilt für den Zusammenhang zwischen Wellenlänge λ und Länge L für stehende Wellen:

$L=\dfrac {\lambda}{2}\cdot n$ mit n = 1, 2, 3, …

Mit der Bedingung, dass sich an den Enden jeweils Knoten befinden müssen, passen also nur ganzzahlige Vielfache der halben Wellenlänge in den Aufenthaltsbereich des Teilchens.

Die Energie des Elektrons ist gleich seiner kinetischen Energie, da wir ja festgelegt haben, dass die potentielle Energie entlang der Länge L Null sein soll.

Es gilt also: $E=E_{kin}=\frac {1}{2}mv^{2}$

Mit $p=mv$ bzw. $p^{2}=m^{2}v^{2}$ lässt sich die kinetische Energie und damit die Gesamtenergie auch ausdrücken als

$E=\dfrac {p^{2}}{2m}$ (1)

Nach De Broglie gilt für die Wellenlänge:

$\lambda=\dfrac {h}{p}$

Für den Zusammenhang zwischen Wellenlänge und Länge L gilt (s.o.):

$L=\dfrac {\lambda}{2}\cdot n$ und damit $\lambda=\dfrac {2L}{n}$

Nun können wir beide Ausdrücke für die Wellenlänge gleichsetzen:

$\dfrac {2L}{n}=\dfrac {h}{p}$

Löst man diese Gleichung nach p auf, erhält man für den Impuls

$p=\dfrac {nh}{2L}$

Diesen Ausdruck für den Impuls setzen wir nun in Gleichung (1) ein und erhalten so für die gesuchte Energie

$E=\dfrac {h^{2}}{8mL^{2}}\cdot n^{2}$ mit $n=1,2,3,...$

Es zeigt sich also:

Die Überlegung führt dazu, dass die Energie nur bestimmte Werte annehmen kann; die Energie ist gequantelt.

Setzt man in die Gleichung für die Energie eine Länge L in der Größenordnung des Durchmessers eines Wasserstoffatoms (10^-10m) ein, so erhält man für die Energie:

$E=\dfrac {\left (6,626\cdot 10^{-34}Js\right )^{2}}{8\cdot 9,109\cdot 10^{-31}kg\cdot \left(10^{-10}m\right)^{2}}\cdot n^{2}$

Berechnet man den Bruch, ergibt sich:

$E=6,02\cdot 10^{-18}J\cdot n^{2}$ bzw. $E=37,6eV\cdot n^{2}$

Für die verschiedenen Energiezustände ergeben sich folgende Energien:

Für n = 1: $E_{1}=37,6eV\cdot 1=37,6eV$

Für n = 2: $E_{2}=37,6eV\cdot 4=150,4eV$

Für n = 3: $E_{3}=37,6eV\cdot 9=338,5eV$ usw.

Die ganze Zahl n wird als Quantenzahl bezeichnet. Aus der Gleichung für die Energie ergibt sich die Tatsache, dass die niedrigste Energie nicht gleich null ist. Dies steht im Gegensatz zur klassischen Physik, in der ein Teilchen sehr wohl die Energie E = 0 haben kann.

Die Energie des niedrigsten Energiezustandes $E_{1}$ wird als Nullpunktsenergie bezeichnet. Daraus folgt die Erkenntnis, dass nach der Quantenmechanik Teilchen auch im absoluten Nullpunkt (0 K) Energie besitzen.

Dies steht im Einklang mit der Unschärferelation, denn aus den Zusammenhängen ergibt sich:

Je kleiner die Breite $L$ des Potentialtopfes, also je kleiner die Ortsunschärfe $\Delta x$ , umso größer muss die Impulsunschärfe $\Delta p$ sein und wegen $E=E_{kin}=\dfrac {p^{2}}{2m}$ auch die Energie.

Was kann man mit diesem Modell anfangen?

Da es sich beim Wasserstoffatom um ein dreidimensionales Gebilde handelt und sich im Gegensatz zum Modell des linearen Potentialtopfes der positiv geladene Atomkern innerhalb des Aufenthaltsbereichs befindet, erhält man mit diesem Modell natürlich nicht die Energien im Wasserstoffatom. Die Größenordnung der berechneten Energien ist jedoch mit den Energiewerten innerhalb von Atomen vergleichbar, wenn man für die Länge L Werte in der Größenordnung des Atomdurchmessers einsetzt.

Entscheidend bei diesem Modell ist, dass sich durch die Beschreibung des Zustandes des Elektrons mit einer stehenden Welle automatisch diskrete Energiewerte ergeben.

Was ändert sich an der Wellenfunktion im Wasserstoffatom?

Die Wellenfunktionen und damit die Wahrscheinlichkeitsverteilungen für den Aufenthalt des Elektrons auf ein dreidimensionales Gebilde zu übertragen, ist gar nicht schwer:

Betrachten wir den Grundzustand, so gilt:

Die Wahrscheinlichkeitsdichte ist in der Mitte der Länge L am größten, nach außen nimmt sie ab. Im dreidimensionalen Raum ergäbe sich eine kugelsymmetrische Verteilung der Wahrscheinlichkeitsdichte – in der Mitte der Kugel ist sie am größten, mit zunehmendem Abstand r vom Kugelmittelpunkt nimmt sie ab.

Im Energiezustand n = 2 dagegen ist die Wahrscheinlichkeitsdichte in der Mitte Null, von dort aus wird sie größer und mit zunehmendem Abstand wieder kleiner. Der Bereich, in dem sich das Elektron aufhalten kann, hat die Form einer Hantel.

Im Atom gibt es eine Zentralladung

Man könnte meinen, dass sich mit dem Atomkern im Zentrum alles ändern würde – doch tatsächlich bleiben die Grundformen der Wellenfunktionen erhalten. Durch die auftretenden Coulomb-Kräfte werden sie lediglich etwas deformiert:

^{Ψ-Funktionen ohne (oben) und mit (unten) Zentralladung}

Die Elektronen bzw. die Oberschwingungen werden vom Kern angezogen. Dadurch nimmt die Aufenthaltswahrscheinlichkeit in Kernnähe zu.

Info:

Die $\psi$ -Funktionen sind Lösungen der Schrödinger-Gleichung für die entsprechenden vorgegebenen Bedingungen.

Kann sich ein Elektron im Kern aufhalten?

Nach dem Bohrschen Atommodell kann sich ein Elektron nur auf bestimmten Bahnen um den Kern herum aufhalten – keinesfalls jedoch im Kern.

Aus den Wellenfunktionen des quantenmechanischen Atommodells ergibt sich nun für den Grundzustand die größte Aufenthaltswahrscheinlichkeitsdichte im Zentrum – also genau dort, wo sich der Kern befindet. Dies klingt nach einem Widerspruch – was bedeutet das?

Betrachten wir dazu die Ψ-Funktion mit Zentralladung im Grundzustand etwas genauer. Das Quadrat der Ψ-Funktion |Ψ|² und damit die Funktion der Wahrscheinlichkeitsdichte hat praktisch die gleiche Form.

Da diese symmetrisch ist, reicht es aus, sie von der Zentralladung (Atomkern) aus in eine Richtung in Abhängigkeit vom Abstand x bzw. r vom Kern zu betrachten:

Das folgende Diagramm zeigt noch einmal in groß den rot markierten Verlauf der Wahrscheinlichkeitsfunktion w für das Wasserstoffatom im Grundzustand:

Aus dem Diagramm lässt sich entnehmen:

Die Wahrscheinlichkeitsdichte w (rote Kurve), und damit die Wahrscheinlichkeit, ein Elektron in einem bestimmten kleinen Teilvolumen ΔV im Abstand r vom Atomkern anzutreffen, nimmt mit wachsendem Abstand zum Kern ab.

Um die Wahrscheinlichkeit w_r (schwarze Kurve) zu ermitteln, dass sich das Elektron in einer Kugelschale mit dem Abstand r zum Kern aufhält, muss man die Wahrscheinlichkeitsdichte w mit dem Schalenvolumen ΔV multiplizieren:

Es gilt: $w(r)=|\psi(r)|^2\cdot \Delta V$

Dicht am Atomkern befindliche Kugelschalen (einer bestimmten Dicke Δr) haben ein kleines Volumen, die Wahrscheinlichkeitsdichte w ist jedoch sehr groß. Genau im Kern (also bei r = 0) existiert kein Volumen – daher ist die Antreffwahrscheinlichkeit für das Elektron im Zentrum praktisch Null.

Weiter entfernte Kugelschalen besitzen (bei gleicher Dicke Δr) zwar ein größeres Volumen, die Wahrscheinlichkeitsdichte w ist jedoch kleiner.

Diese Überlegung legt nahe:

Es existiert für das Wasserstoffatom ein Maximalwert für die Antreffwahrscheinlichkeit w_r für einen bestimmten Radius.

Und das Erstaunliche ist: Dieser Radius entspricht genau dem Bohrschen Radius r_B!

Während sich das Elektron nach dem Bohrschen Atommodell nur genau auf diesem Radius aufhalten kann, ergibt sich im quantenmechanischen Atommodell dieser Radius als der Abstand mit der größten Aufenthaltswahrscheinlichkeit.

Das Orbitalmodell

Das Orbitalmodell ergibt sich letztendlich aus dem Versuch, die Bereiche verschiedener Aufenthaltswahrscheinlichkeitsdichten bildlich zu veranschaulichen.

Die räumlichen Wahrscheinlichkeitsverteilungen der Elektronen in der Atomhülle werden als Orbitale bezeichnet. Wie genaue Rechnungen zeigen, können bis auf den Grundzustand zu einer bestimmten Hauptquantenzahl n mehrere, voneinander verschiedene räumliche Wahrscheinlichkeitsverteilungen existieren. Diese verschiedenen Orbitale klassifiziert man durch Nebenquantenzahlen l und m.

Darüber hinaus kann ein Elektron unabhängig von seiner Wahrscheinlichkeitsverteilung im Raum noch selbst zwei Energiezustände annehmen, die durch die Spinquantenzahl s charakterisiert werden.

In der Darstellung von Orbitalen werden die Bereiche, in denen sich das Elektron aufhalten kann, eingefärbt. Je größer die Aufenthaltswahrscheinlichkeit, umso intensiver die Einfärbung.

In der Regel wird der Raumbereich eingefärbt, in dem die Aufenthaltswahrscheinlichkeit 90% beträgt.

Das Orbital für das Wasserstoffatom im Grundzustand hat eine kugelsymmetrische Form.

Eine schöne Visualisierung des Wasserstoffatoms in den verschiedenen Energiezuständen und sogar der Übergänge zwischen zwei Energiezuständen findest Du hier:

http://www.hydrogenlab.de

weiter mit Schrödingergleichung

zurück