Bewegte Ladungsträger im Magnetfeld

Wie verhalten sich bewegte Ladungsträger in einem Magnetfeld?

Wir wollen nun untersuchen, wie sich bewegte Elektronen verhalten, die in ein Magnetfeld gelangen.

Außerdem wollen wir überlegen, ob durch die Ablenkung von Elektronen im Magnetfeld die Elektronenmasse bestimmbar ist – dies war durch die Ablenkung im elektrischen Feld nicht möglich, da die Geschwindigkeit der Elektronen nicht ohne deren Masse bestimmbar ist.

Außerdem ist die Ablenkung von Elektronen mit einer bestimmten Geschwindigkeit im elektrischen Feld von der Elektronenmasse unabhängig.

Zur Erinnerung:

Für die Geschwindigkeit von Elektronen, die mit der Spannung U beschleunigt wurden, gilt:

$v=\sqrt {\dfrac {2Ue}{m_{e}}}$

Die Kraft auf Elektronen im Magnetfeld beträgt

$F_{L}=Bev$

Durch Umstellen dieser Gleichung nach v ergibt sich

$v=\dfrac {F_{L}}{Be}$

Damit haben wir eine zweite Gleichung für die Geschwindigkeit, die sich aus der Kraftwirkung auf Elektronen im Magnetfeld ergibt.

Vielleicht lassen sich beide Gleichungen miteinander verknüpfen?

Dazu soll zunächst das Verhalten von Elektronen im Magnetfeld untersucht werden.

Untersuchung von Elektronen im Magnetfeld

Vorüberlegung:

Während Elektronen innerhalb eines elektrischen Feldes immer parallel zur Feldlinienrichtung beschleunigt / abgelenkt werden, wirkt die Lorentzkraft immer senkrecht zur Bewegungsrichtung der Elektronen und senkrecht zum Magnetfeld.

Das bedeutet:

Ändert sich die Bewegungsrichtung der Elektronen, so ändert sich auch die Richtung der Lorentzkraft.

Versuch:

In einem sogenannten Fadenstrahlrohr lässt sich die Bahn von Elektronen untersuchen. Die Elektronenbahn wird durch ein sich darin befindliches Gas sichtbar gemacht – treffen die Elektronen auf die Gasmoleküle, so leuchten diese auf.

Das Fadenstrahlrohr enthält eine Elektronenkanone, in der Elektronen mit Hilfe einer Spannung zwischen 0 und 300V beschleunigt werden können.

Durch eine spezielle Spulenanordnung (Helmholtz-Spulenpaar) wird ein nahezu homogenes Magnetfeld erzeugt, welches das Fadenstrahrohr durchsetzt.

Versuchsaufbau:

Das Helmholtz-Spulenpaar besteht aus zwei Spulen, deren Abstand gleich dem Spulenradius ist. Die Spulen erzeugen durch Überlagerung ihrer Felder so ein weitgehend homogenes Magnetfeld, welches die gesamte Röhre umfasst. Dazu muss der Erregerstrom I_err in beiden Spulen in die gleiche Richtung fließen.

Je nach Stromrichtung zeigen die Magnetfeldlinien in der Abbildung entweder nach hinten oder nach vorne.

Die magnetische Feldstärke des erzeugten Feldes hängt ab von

Erregerstromstärke I_err (variabel)
Windungszahl n (fest)
Spulenradius R (fest)

Da Windungszahl n und Spulenradius R nicht veränderlich sind, lässt sich nur über die Erregerstromstärke die magnetische Feldstärke einstellen.

Die magnetische Feldstärke innerhalb der Helmholtz-Spulenanordnung lässt sich mit Hilfe des Biot-Savart-Gesetzes herleiten. Damit ergibt sich folgender Zusammenhang:

$B=\mu_{0}\cdot \dfrac {8}{\sqrt {125}}\cdot \dfrac {n\cdot I}{R}$

Die Herleitung findet man u.a. auf der Wikipedia-Seite zur Helmholtz-Spule.

In der Versuchsanleitung von Phywe findet man die folgende Formel, die der oben genannten entspricht:

$B=\dfrac {\mu_{0}\cdot 0,715\cdot n}{R}\cdot I_{err}$

Durch Einsetzen der Spulendaten (Spulenradius $R$ und Windungszahl $n$ ) lässt sich so die magnetische Feldstärke in Abhängigkeit von der Erregerstromstärke berechnen.

Durchführung

Die Beschleunigungsspannung wird auf einen Wert von ca. 250-300V eingestellt. Um den Elektronenstrahl erkennen zu können, muss der Raum vollständig abgedunkelt werden.

Der Elektronenstrahl ist nach unten gerichtet und verläuft zunächst geradlinig:

Anschließend wird die Erregerstromstärke und damit die magnetfische Feldstärke langsam vergrößert.

Beobachtung

Steht das Magnetfeld senkrecht zur Bewegungsrichtung der Elektronen, beschreiben die Elektronen eine Kreisbahn:

Steht das Magnetfeld nicht ganz senkrecht zur Bewegungsrichtung der Elektronen, beschreiben sie eine spiralförmige Bahn.

Folgendes Bild zeigt die Sicht von oben:

Diese Schraubenbahn kommt dadurch zustande, dass es eine zum Magnetfeld senkrechte und eine parallele Komponente der Geschwindigkeit gibt.

In folgendem Video von Phywe kannst Du Dir die Durchführung dieses Versuchs noch einmal anschauen:

Wie kann man durch die Untersuchung von Elektronen im Magnetfeld die Masse eines Elektrons bestimmen?

Wir erstellen eine Skizze, in der sowohl Elektronenbahn (rot) als auch das Magnetfeld (grün) eingezeichnet ist:

Erklärung der Kreisbahn:

Die Lorentzkraft steht immer senkrecht zur Bewegungsrichtung der Elektronen. Dadurch werden die Elektronen auf eine Kreisbahn gezwungen. Die Lorentzkraft ist stets zum Kreismittelpunkt gerichtet und wirkt daher als Zentripetalkraft.

Je stärker das Magnetfeld ist, umso größer ist die Lorentzkraft und umso kleiner ist damit der Radius der Kreisbahn.

Die Lorentzkraft F_L wirkt als Zentripetalkraft F_Z und zwingt die Elektronen auf eine Kreisbahn mit dem Radius r.

In jedem Punkt der Kreisbahn gilt also:

$F_{Z}=F_{L}$

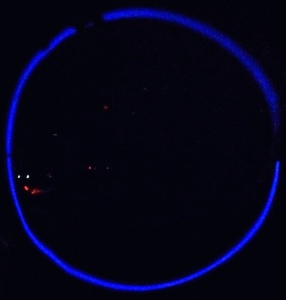
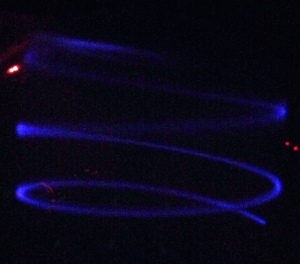
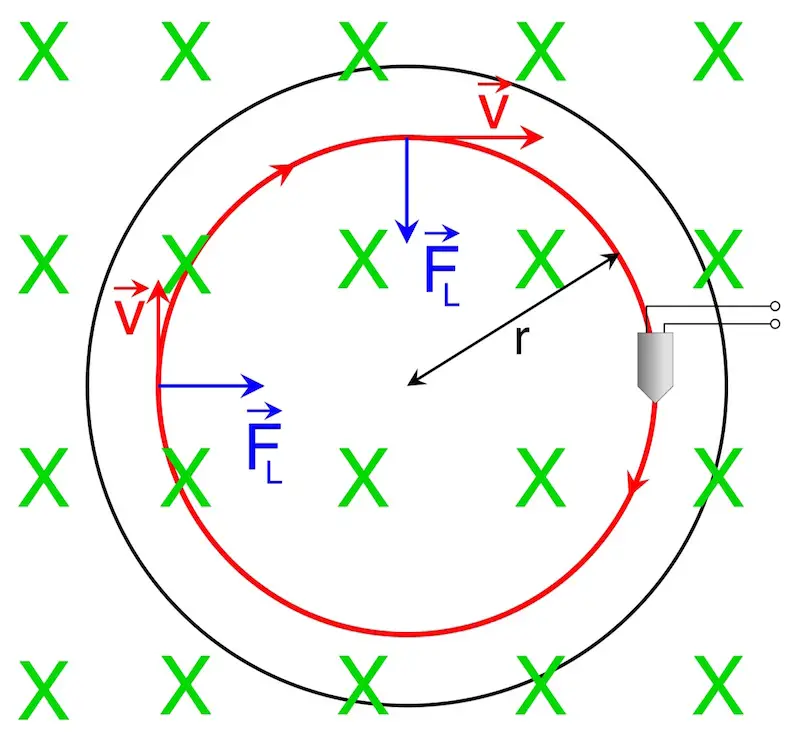
Zur Erinnerung: Für die Zentripetalkraft gilt: 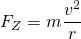$F_{Z}=m\dfrac {v^{2}}{r}$

In diesem Fall ist die Masse die gesuchte Elektronenmasse m_e, und v ist der zum Magnetfeld senkrechte Anteil der Geschwindigkeit der Elektronen v_s.

Es gilt also: 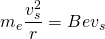$m_{e}\dfrac {v_{s}^{2}}{r}=Bev_{s}$

Hinweis:

Die Zentripetalbeschleunigung a_z bewirkt nur eine Richtungsänderung. Der Betrag der Geschwindigkeit bleibt konstant. Steht das Magnetfeld senkrecht zur Geschwindigkeit, verrichtet es keine Arbeit.

Nun lösen wir die oben aufgestellte Gleichung nach m_e auf und erhalten:

$m_{e}=\dfrac {Bev_{s}r}{v_{s}^{2}}$

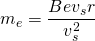
Kürzen mit v_s ergibt

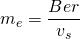$m_{e}=\dfrac {Ber}{v_{s}}$ (1)

Welche Größen dieser Gleichung sind bekannt, welche können bestimmt werden?

Wenn es möglich ist, alle Größen in Gleichung (1) zu bestimmen, lässt sich die Elektronenmasse berechnen.

Eine Analyse aller Größen ergibt:

Elementarladung e:

→ bekannt aus Millikan-Experiment

Magnetische Feldstärke B:

→ kann mit einer Hallsonde gemessen oder mit Hilfe der Formel aus der Versuchsanleitung (s.o.) berechnet werden.

Radius r der Kreisbahn:

→ kann mit Hilfe von Markierungen im Fadenstrahlrohr abgelesen werden.

Geschwindigkeit v_s der Elektronen:

Die Geschwindigkeit, mit der die Elektronen die Anode verlassen, ist nicht bekannt, aber mit Hilfe des Ansatzes der Energieerhaltung (E_kin = E_el) haben wir bereits folgenden Zusammenhang hergeleitet (s.o.):

Es gilt: 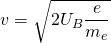$v=\sqrt {2U_{B}\dfrac {e}{m_{e}}}$ (2)

Aufstellen der Gleichung zur Berechnung der Elektronenmasse

Nun setzen wir den Zusammenhang für die Geschwindigkeit (2) in Gleichung (1) ein.

Um die Wurzel loszuwerden, werden zunächst beide Gleichungen quadriert:

Quadrieren von Gleichung (1) ergibt

$v_{s}^{2}=2U\dfrac {e}{m_{e}}$

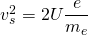
Quadrieren von Gleichung (2) ergibt

$m_{e}^{2}=\dfrac {B^{2}e^{2}r^{2}}{v_{s}^{2}}$

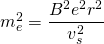
Setzt man nun den Ausdruck von v_s² in die quadrierte Gleichung (1), erhält man

$m_{e}^{2}=\dfrac {B^{2}e^{2}r^{2}m_{e}}{2U_{B}e}$

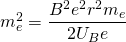
Nun kann man e und m_e kürzen und erhält schließlich für die Elektronenmasse

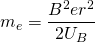$m_{e}=\dfrac {B^{2}er^{2}}{2U_{B}}$ (3)

Alle Größen auf der rechten Seite können gemessen werden. Mit dieser Gleichung lässt sich also die gesuchte Elektronenmasse berechnen.

Magnetische Feldstärke B

Die magnetische Feldstärke B kann entweder mit einer Hallsonde gemessen und direkt in die Gleichung eingesetzt oder mit der Formel aus der Versuchsanleitung (s.o.) berechnet werden:

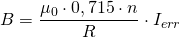$B=\dfrac {\mu_{0}\cdot 0,715\cdot n}{R}\cdot I_{err}$ (4)

Darin ist R der Spulenradius der Helmholtzspulen (man benutzt einen Großbuchstaben, um den Spulenradius vom Radius der Kreisbahn der Elektronen zu unterscheiden).

Um mit dieser Gleichung die magnetische Feldstärke ermitteln zu können, müssen zunächst Windungszahl n und Spulenradius R durch Abzählen bzw. Messen bestimmt werden.

Die Bestimmung ergibt:

R = 20cm

n = 154

Misst man nun die Erregerstromstärke I_err, kann die magnetische Feldstärke berechnet werden.

Vorgehensweise zur Ermittlung der Elektronenmasse

Es wird eine feste Beschleunigungsspannung eingestellt und anschließend die Erregerstromstärke so eingestellt, dass der Elektronenstrahl eine der Markierungen im Fadenstrahlrohr streift. Die Markierungen sind so angebracht, dass die Radien 2, 3, 4 und 5cm recht genau eingestellt werden können.

Für jeden Radius wird die benötigte Erregerstromstärke abgelesen. Daraus kann anschließend mit Hilfe von Gleichung (4) die magnetische Feldstärke berechnet werden.

Eine Überprüfung der Feldstärke mit einer Hallsonde ergibt weitgehend die gleichen Werte.

Messwerte:

Folgende Werte bleiben konstant:

R = 20cm

n = 154

U_B = 250V

Die folgenden Tabelle enthält Beispielwerte für die variablen Messwerte sowie die daraus berechneten Werte für die magnetische Feldstärke und die Elektronenmasse:

r in m	I_err in A	B in mT	m_e in 10^-31kg
0,02	3,93	2,72	9,48
0,03	2,53	1,75	8,83
0,04	1,94	1,34	9,20
0,05	1,53	1,06	9,0

Beispielrechnung:

Für die erste Zeile (r = 0,02m und I_err = 3,93A) ergeben sich folgende Werte:

1. Berechnung der magnetischen Feldstärke aus der Erregerstromstärke

$B=\dfrac {1,2566\cdot 10^{-6}\frac {Vs}{Am}\cdot 0,715\cdot 154}{0,2m}\cdot 3,93A=2,72\cdot 10^{-3}T=2,72mT$

2. Berechnung der Elektronenmasse

$m_{e}=\dfrac {(2,72\cdot 10^{-3}T)^{2}\cdot 1,602\cdot 10^{-19}C\cdot (0,02m)^{2}}{2\cdot 250V}=9,48\cdot 10^{-31}kg$

Aus den Ergebnissen der vier Messreihen lässt sich nun der Mittelwert für die Elektronenmasse berechnen. Dieser ergibt sich aus dem Quotienten der Summe aller Massen und der Anzahl der Messungen.

Der Mittelwert beträgt:

$m_{e}=9,18\cdot 10^{-31}kg$

Der Literaturwert für die Elektronenmasse beträgt:

$m_{e}=9,109\cdot 10^{-31}kg$

Um unser Messergebnis besser beurteilen zu können, lässt sich zusätzlich die prozentuale Abweichung berechnen.

Die prozentuale Abweichung ergibt sich aus dem Quotienten der absoluten Abweichung und des Literaturwertes:

$\dfrac {absolute\ Abweichung}{Literaturwert}\cdot 100\%$ = Abweichung in $%$

$\dfrac {(9,18 - 9,109)\cdot 10^{-31}kg}{9,109\cdot 10^{-31}kg}=0,008=0,8\%$

Das Messergebnis ist, vor allem wenn man die Größenordnung der Elektronenmasse berücksichtigt, als sehr gut zu bezeichnen.

Spezifische Ladung von Elektronen

In den meisten Physikbüchern wird mit Hilfe des Versuchs mit dem Fadenstrahlrohr anstelle der Elektronenmasse die sogenannte spezifische Ladung eines Elektrons ermittelt.

Darunter versteht man den Quotienten aus Ladung und Masse $\dfrac {e}{m}$ . Die Einheit lautet $\dfrac {C}{kg}$ .

Die spezifische Ladung gibt praktisch an, welche Ladung 1kg Elektronen haben.

Der Literaturwert der spezifischen Ladung für Elektronen beträgt

$\dfrac {e}{m}=1,759\cdot 10^{11}\frac {C}{kg}$

Berechnung der Geschwindigkeit der Elektronen

Da nun die Elektronenmasse bekannt ist, kann auch die Geschwindigkeit der Elektronen nach ihrer Beschleunigung im elektrischen Feld berechnet werden.

Für die Geschwindigkeit gilt (s.o.):

$v=\sqrt {2U_{B}\dfrac {e}{m_{e}}}$

Die Beschleunigungsspannung betrug in unserem Versuch U_B = 250V. Daraus ergibt sich folgende Geschwindigkeit:

$v=\sqrt {2\cdot 250V\cdot \dfrac {1,602\cdot 10^{-19}C}{9,109\cdot 10^{-31}kg}}=9.377.367\dfrac {m}{s}$

Das entspricht ca. 3% der Lichtgeschwindigkeit.

Beim Versuch mit der Elektronenstrahlablenkröhre haben wir Beschleunigungsspannungen von ca. 5kV benutzt. Das ist das 20-fache der in diesem Versuch verwendeten Spannung von 250V.

Da die Beschleunigungsspannung in der Formel für die Geschwindigkeit unter der Wurzel steht, vergrößert sich die Geschwindigkeit bei einer Verzwanzigfachung der Beschleunigungsspannung um den Faktor $\sqrt {20}$ = 4,47.

Die Geschwindigkeit der Elektronen betrug dort also etwa 42.000.000 m/s. Das sind knapp 14% der Lichtgeschwindigkeit.

Elektronen schneller als das Licht?

Wenn die Formel für die Geschwindigkeit uneingeschränkt gültig ist, dürfte es kein Problem sein, Elektronen auf Überlichtgeschwindigkeit zu beschleunigen. Um die Beschleunigungsspannung zu berechnen, die notwendig wäre, um Elektronen auf Lichtgeschwindigkeit zu beschleunigen, muss man nur die Formel nach U_B umstellen und für die Geschwindigkeit die Lichtgeschwindigkeit c einsetzen:

$U_{B}=\dfrac {c^{2}m_{e}}{2e}=255,5kV$

Es ergibt sich eine Beschleunigungsspannung von knapp 256 kV. Diese Spannung ist zwar größer als die, die wir im Unterricht erzeugen können, technisch ist es aber kein Problem, Elektronen mit dieser oder noch höherer Spannung zu beschleunigen.

Trotzdem erreichen die Elektronen auch mit dieser Beschleunigungsspannung nicht die Lichtgeschwindigkeit, denn bei sehr hohen Geschwindigkeiten treten relativistische Effekte auf: Die Elektronen verhalten sich so, als würde ihre Masse zunehmen, was zur Folge hat, dass immer mehr Energie benötigt wird, um sie weiter zu beschleunigen. Man spricht von relativistischer Massenzunahme.

Genauere Informationen zu diesem Thema findest Du im Themenbereich “Relativitätstheorie“.

Dieser Effekt spielt allerdings erst bei sehr hohen Geschwindigkeiten eine Rolle. Bis zu einer Beschleunigungsspannung von ca. 10kV kann mit konstanter Masse gerechnet werden (die Geschwindigkeit der Elektronen beträgt dann knapp 20% der Lichtgeschwindigkeit). Hier liegt der Fehler bei ca. 1,5%.

Relativistische Masse / Ruhemasse

Bei Objekten mit sehr hoher Geschwindigkeit muss aufgrund der relativistischen Effekte mit der relativistischen Masse gerechnet werden.

Die Elektronenmasse, die man in Formelsammlungen findet (s. Literaturwert oben), wird als Ruhemasse bezeichnet.

Übungsaufgaben:

Metzler Physik SII (3. Auflage 1998)

S. 232 1. / 2. (/ 3. / 4.)

weiter mit Inhomogene Magnetfelder

zurück