Das quantenmechanische Atommodell
Die Annahme der Existenz bestimmter Elektronenbahnen war mit den Erkenntnissen der Quantenphysik nicht vereinbar. Eine moderne Atomtheorie muss die Eigenschaften von Quantenobjekten berücksichtigen. Das führt letztendlich dazu, dass man nicht genau angeben kann, wo sich ein Elektron genau befindet. Man kann lediglich Wahrscheinlichkeiten für den Aufenthaltsort angeben.
Damit beseitigt das quantenmechanische Atommodell die Probleme der klassischen Atommodelle – allerdings zu einem recht hohen Preis: Es ist nicht mehr anschaulich, und jede bildliche Vorstellung führt zu Problemen.
Die Entwicklung eines quantenmechanischen Atommodells beruht auf folgenden Erkenntnissen:
- Elektronen verhalten sich nicht wie kleine Teilchen, sondern gehorchen als sog. Quantenobjekte eigenen, der Anschauung kaum zugänglichen Regeln.
- Elektronen können weder mit dem Teilchen- noch mit dem Wellenmodell angemessen erfasst werden.
- Über das Verhalten von Mikroobjekten können nur Wahrscheinlichkeitsaussagen getroffen werden.
Da die klassische Physik im atomaren Bereich versagt, verzichtet man auf nicht nachprüfbare Annahmen und beschränkt sich auf das, was beobachtbar ist:
Beobachtbar sind lediglich Photonen, die ein Atom absorbiert bzw. emittiert sowie die Intensitätsverteilung zwischen den einzelnen Spektrallinien.
Quantenmechanische Atommodelle sind mathematische Modelle
Im Jahre 1925 entwickelte Werner Heisenberg ein völlig neues Konzept (die sog. Matrizenmechanik), welches vollständig auf Anschaulichkeit verzichtet. Dabei handelt es sich um einen abstrakten mathematischer Formalismus.
Dieses quantenmechanische Atommodell ist ein rein mathematisches Modell. Alle bildhaften Darstellungen sind problematisch und führen nicht selten zu falschen Vorstellungen.
Die Ergebnisse von Heisenberg entsprechen denen von Erwin Schrödingers 1926 formulierten Wellenmechanik, die ein wenig anschaulicher und eher verständlich ist:
- Schrödinger benutzt die Vorstellung, dass die Ausbreitung eines Elektrons durch eine De-Broglie-Welle mit einer von Zeit und Raum abhängigen Amplitude beschrieben werden kann.
- Atomare Teilchen können nur durch eine
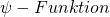beschrieben werden, deren Betragsquadrat 
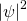proportional zur Wahrscheinlichkeit ist, das Teilchen nachzuweisen.
- Einem stationären Zustand des Elektrons mit einer von der Zeit unabhängigen Amplitudenverteilung entspricht danach einer dreidimensionalen stehenden Welle.
In der damaligen Zeit (1926) gab es nur sehr begrenzte Möglichkeiten zur Überprüfung; inzwischen ist die Richtigkeit der Ergebnisse aus Schrödingers Theorie aber vielfach experimentell bestätigt worden.
Die Schrödingergleichung
Mit der von Schrödinger formulierten und nach ihm benannten Schrödinger-Gleichung gelingt die vollständige und widerspruchsfreie Beschreibung von Quantensystemen, wie Atomen, Molekülen und Festkörpern.
Dafür erhielt Erwin Schrödinger im Jahre 1933 den Nobelpreis für Physik.
Allerdings ist schon die Beschreibung von Systemen mit wenigen Teilchen mathematisch sehr anspruchsvoll.
Die Grundidee von Schrödinger war, die Elektronen nicht als Teilchen sondern als Welle mit der De-Broglie-Wellenlänge aufzufassen. Die Schrödinger-Gleichung ist eine der klassischen Wellengleichung ähnlichen Gleichung, mit der sich die Wahrscheinlichkeit, Teilchen in einem bestimmten Raumvolumen nachzuweisen, beschreiben und berechnen lässt.
Schrödinger griff De Broglies Vorstellung von der stehenden Elektronenwelle um den Atomkern auf, führte diesen Gedankengang jedoch weiter und dachte sich stattdessen ein räumlich ausgedehntes Gebilde, welches in Form einer stehenden Welle schwingen kann.
Mit der Schrödingergleichung lassen sich die Wahrscheinlichkeiten berechnen, ein Elektron in einem bestimmten Abstand vom Kern anzutreffen. Außerdem ergeben sich aus den Lösungen der Schrödingergleichung die diskreten Energieniveaus.
Eine ausführliche Heranführung an die Schrödingergleichung sowie die Anwendung zur Berechnung von Energiezuständen und Wahrscheinlichkeiten folgt im letzten Kapitel dieses Themenbereichs “Die Schrödingergleichung“.
Um ein Verständnis dafür zu bekommen, wie Schrödinger den Aufenthalt von Elektronen in einem Atom mit Hilfe einer Wellenfunktion beschrieben hat, werden zunächst einfache Fälle betrachtet und die Ergebnisse daraus anschließend auf ein Atom übertragen.
Beschreibung des Aufenthalts eines Elektrons
Grundlage der Beschreibung des Aufenthalts eines Elektrons in einem bestimmten Bereich ist folgende Überlegung:
Ein frei bewegliches Elektron kann durch eine fortlaufende Welle beschrieben werden. Ein in einem bestimmten Bereich (z.B. in einem Atom) eingesperrtes Elektron muss dagegen durch eine stehende Welle beschrieben werden.
Weil sich das Elektron nicht außerhalb des definierten Bereichs aufhalten kann, müssen seine Aufenthaltswahrscheinlichkeit und die Amplitude dieser Wellenfunktion auf den Bereich des Atoms beschränkt sein.
Mit anderen Worten:
Die Wahrscheinlichkeit, dass sich das Elektron irgendwo in diesem Bereich aufhält, ist 1. Man spricht dabei von einer Normierung.
(Normierungsbedingung: Das Elektron muss sich mit der Wahrscheinlichkeit 1 irgendwo im vorgegebenen Raumbereich befinden.)
Vereinfachung auf eine Dimension
Um den Aufenthalt eines Teilchens in einem bestimmten Bereich, z.B. im Bereich eines Atoms oder Moleküls, zu beschreiben, nimmt man einen solchen Bereich der Einfachheit halber zunächst nicht räumlich, sondern eindimensional an. In diesem Bereich soll sich das Teilchen kräftefrei bewegen, aber nicht nach außen gelangen können.
Ein Modell, welches den Aufenthalt eines Elektrons in einem bestimmten eindimensionalen Bereich beschreibt, ist das Modell des linearen Potentialtopfes.
