Grundlagen zur Schrödingergleichung

Grundlagen zum Verständnis der Schrödingergleichung

1. Klassische Wellengleichung

2. Die Wellenfunktion (Ψ-Funktion)

3. Differentialgleichungen

4. Komplexe Zahlen und Eulersche Formel

5. Operatoren und partielle Ableitungen

1. Die klassische Wellengleichung

Die eindimensionale Wellengleichung einer fortschreitenden (sich in positive x-Richtung bewegenden) Sinuswelle lautet:

$y(x,t)=y_{max}\cdot sin \left[2\pi\left(\dfrac {t}{T}-\dfrac {x}{\lambda}\right) \right]$

In dieser Form wird die Auslenkung am Ort $x=0$ mit der Zeit zunächst negativ. Für die entgegengesetzte Ausrichtung entsprechend würde gelten:

$y(x,t)=y_{max}\cdot sin \left[2\pi\left(\dfrac {x}{\lambda}-\dfrac {t}{T}\right) \right]$

(Beide Formen sind völlig gleichberechtigt.)

Die Wellengleichung enthält die Abhängigkeit des Schwingungszustandes eines Oszillators auf dem Wellenträger von der Zeit $t$ und vom Abstand $x$ vom Erreger.

Für einen stationären Zustand (also für eine stehende Welle) gibt es nur eine Ortsabhängigkeit.

Für diesen Fall lautet die Wellengleichung:

$y(x)=y_{max}\cdot sin \left(2\pi\dfrac {x}{\lambda}\right)$

(Wie oben bereits beschrieben, kann das Vorzeichen der Auslenkung willkürlich gesetzt werden – bei der Aufenthaltswahrscheinlichkeit ist sowieso nur das Quadrat der Wellenfunktion von Bedeutung).

Die Wellenfunktion $\Psi(x)$ für den linearen Potentialtopf entspricht genau dieser Funktion einer stehenden Welle.

Für diesen Fall können wir also schreiben:

$\Psi(x)=y_{max}\cdot sin \left(\dfrac {2\pi x}{\lambda}\right)$

mit der Bedingung $L=n\cdot \dfrac {\lambda}{2}$ bzw. $\lambda=\dfrac {2L}{n}$

(In den Topf der Breite $L$ passen nur ganzahlige Vielfache der halben Wellenlänge.)

2. Die Wellenfunktion (Ψ-Funktion)

Die Bedeutung der Wellenfunktion wurde bereits im Abschnitt zum Jönsson-Experiment sowie zum linearen Potentialtopf erläutert. Hier noch einmal die wichtigsten Zusammenhänge:

Die Intensität $I$ von Licht ist ein Maß für die Anzahl der registrierten Photonen pro Zeit- und Flächeneinheit: Die Anzahl der registrierten Photonen ist proportional zur Intensität $I$ und damit proportional zum Quadrat der Amplitude der elektrischen Feldstärke $\widehat {E}^{2}$ . Es gilt also $I\sim \widehat {E}^{2}$
Das Quadrat der elektrischen Feldstärke $\widehat {E}^{2}(x,y,t)$ ist proportional zur Wahrscheinlichkeit, ein Photon an der Stelle (x,y) zur Zeit t zu registrieren.
Bei Materieteilchen, wie z.B. Elektronen, tritt an die Stelle der (Auslenkung der) elektrischen Feldstärke die Wellenfunktion, der das Symbol $\psi$ (der griechische Buchstabe “psi”) zugeordnet ist. Das Verhalten von Elektronen oder anderen Quantenobjekten wird also durch die Wellenfunktion $\psi (x,y,z,t)$ beschrieben, deren Quadrat proportional zur Wahrscheinlichkeit ist, ein Teilchen zu einer bestimmten Zeit $t$ an einem bestimmten Ort $(x,y,z)$ anzutreffen.
Das Produkt aus dem Betragsquadrat der Wellenfunktion $\left |\psi (r,t)\right |^{2}$ und dem Volumenelement $\Delta V$ gibt die Antreffwahrscheinlichkeit eines Teilchens $w(r,t)= \left |\psi (r,t)\right |^{2}\cdot \Delta V$ in einem Raumvolumen $\Delta V$ in der Umgebnung vom Ort $r$ in Abhängigkeit von der Zeit $t$ an.

Die $\psi$ -Funktion beschreibt damit den quantenmechanischen Zustand eines Elementarteilchens.

3. Differentialgleichungen

Da es sich bei der Schrödingergleichung um eine Differentialgleichung (abgekürzt: DGL) handelt, sollte man wissen, was man unter einer Differentialgleichung versteht, und was es bedeutet, eine Differentialgleichung zu lösen.

Unter einer Differentialgleichung versteht man eine Gleichung, in der neben einer Funktion auch Ableitungen dieser Funktion (sowie unabhängige Variablen) erscheinen.

Ein Beispiel für eine Differentialgleichung, die sich aus einem physikalischen Sachverhalt ergibt, ist die Differentialgleichung einer harmonischen Schwingung:

Bei einer harmonischen Schwingung ist die rücktreibende Kraft $F_{R}$ proportional zur Auslenkung (Elongation).

Es gilt also $F_{R}\sim s$ und damit das lineare Kraftgesetz:

$F_{R}=-Ds$ mit $D$ = Richtgröße

Die Rückstellkraft ist der Elongation entgegengerichtet. Bei einer Feder ist $D$ die Federkonstante.

Außerdem gilt allgemein und damit für jeden Zeitpunkt der Schwingung:

$F=ma$ (Grundgleichung der Mechanik)

Damit gilt: $ma=-Ds$

und für die Beschleunigung ergibt sich:

$a=-\dfrac {D}{m}\cdot s$ (1)

Sowohl die Beschleunigung $a$ als auch die Elongation $s$ sind zeitabhängig, also Funktionen der Zeit.

Dabei gilt: $a(t)=\dot v(t)=\ddot s(t)$

Die Beschleunigung ist die zweite Ableitung des Weges (hier: Elongation) nach der Zeit. Wir können also für Gleichung (1) schreiben:

$\ddot s(t)=-\dfrac {D}{m}\cdot s(t)$

Damit haben wir eine Differentialgleichung. Der Quotient $\dfrac {D}{m}$ ist für einen bestimmten Oszillator konstant und kann daher durch eine Konstante $k$ ersetzt werden. Dann lautet die Differentialgleichung:

$\ddot s(t)=-k\cdot s(t)$ bzw. $\ddot s(t)+k\cdot s(t)=0$

Dies ist die Differentialgleichung einer harmonischen Schwingung.

Wie löst man eine Differentialgleichung?

Eine Differentialgleichung zu lösen, bedeutet, eine Funktion – in diesem Fall eine Funktion $s(t)$ – zu finden, die die Differentialgleichung erfüllt. Durch das Einsetzen einer solchen Lösungsfunktion ergeben sich dann bestimmte Bedingungen, z.B. lassen sich daraus bestimmte Energiewerte berechnen.

Schauen wir uns die DGL einmal an und überlegen: Die Bedingung für die gesuchte Funktion lautet:

“Die gesuchte Funktion $s(t)$ , multipliziert mit dem Faktor $-k$ soll gleich der zweiten Ableitung dieser Funktion sein.”

Man kann nun raten, welche Funktion diese Bedingung erfüllen könnte.

In diesem Fall ist es einfach:

Eine mögliche Funktion ist die Sinusfunktion (die zweite Ableitung der Sinusfunktion ist $-sin$ ).

Für dieses Beispiel ist die Lösungsfunktion schon bekannt. Es handelt sich um die Schwingungsgleichung einer harmonischen Schwingung:

$s(t)=\widehat{s} \cdot sin\, \omega t$ bzw. $s(t)=sin\, \omega t$ (für $\widehat{s} =1$ )

Dabei ist $\widehat{s}$ die Amplitude. Der Einfachheit soll die Amplitude $\widehat{s} =1$ betragen. Dann lautet die zweite Ableitung dieser Funktion

$\ddot s(t)=-\omega^{2}\cdot sin \, \omega t$

Setzt man nun diese Funktion bzw. ihre zweite Ableitung in die DGL ein, so ergibt sich:

$-\omega ^{2}\cdot sin \, \omega t=-k\cdot sin \, \omega t$

Diese Gleichung ist erfüllt, wenn gilt:

$k=\omega ^{2}$ , also $\dfrac {D}{m}=\omega ^{2}$ bzw. $\omega=\sqrt {\dfrac {D}{m}}$

Eine mögliche Lösungsfunktion für die Differentialgleichung $\ddot s(t)=-k\cdot s(t)$ lautet also

$s(t)=sin \, \omega t$ mit $\omega=\sqrt {\dfrac {D}{m}}$

Hätte man als Lösungsfunktion die entsprechende Kosinusfunktion geraten, hätte es ebenfalls geklappt.

Auch die Funktion $s(t)=cos \, \omega t$ stellt also eine mögliche Lösungsfunktion dar.

Alternative Lösung mit komplexer e-Funktion

Es gibt noch eine weitere Funktion, die eine Lösung der o.g. Differentialgleichung darstellt, und zwar die Funktion

$s(t)=e^{i\omega t}$ wobei gelten soll: $i=\sqrt {-1}$ bzw. $i^{2}=-1$

Es handelt sich bei “ $i$ ” um eine sogenannte imaginäre Zahl (bzw. die imaginäre Einheit). Imaginäre Zahlen gehören zu den komplexen Zahlen. Was man darunter versteht, erfährst Du im nachfolgenden Abschnitt 4. Nehmen wir die o.g. Definition erst einmal hin und überprüfen, ob die genannte Funktion tatsächlich eine Lösung der DGL darstellt:

Wir setzen also in die Differentialgleichung in der Form $\ddot s(t)+k\cdot s(t)=0$ (s.o.) die genannte Funktion sowie ihre zweite Ableitung ein.

Die zweite Ableitung dieser Funktion lässt sich schreiben als $\dfrac {d^{2}}{dt^{2}}\left ( e^{i \omega t}\right )$

Info: $\dfrac {d^{2}}{dt^{2}}$ ist eine Rechenvorschrift und bedeutet, das man alles, was dahinter steht,

zweimal nach der Zeit ableiten soll

Damit lautet die Differentialgleichung:

$\dfrac {d^{2}}{dt^{2}}\left(e^{i\omega t}\right)+k\cdot e^{i\omega t}=0$

Leitet man nun die Funktion $e^{i\omega t}$ entsprechend der Rechenvorschrift (mit Hilfe der Kettenregel) zweimal ab, so ergibt sich

$i^{2} \omega^{2} \cdot e^{i \omega t}+k\cdot e^{i \omega t}=0$

Mit $i^{2}=-1$ (s.o.) folgt: $\omega ^{2}=k$ und damit $\omega=\sqrt {k}$ bzw. $\omega=\sqrt {\dfrac {D}{m}}$ (s.o.)

Damit haben wir gezeigt:

Die Funktion $s(t)=e^{i\omega t}$ ist ebenfalls eine Lösung der Differentialgleichung mit der gleichen Bedingung, die sich auch mit der Sinusfunktion ergeben hat.

4. Komplexe Zahlen und Eulersche Formel

Komplexe Zahlen bestehen aus einem Realteil und einem Imaginärteil.

Für eine komplexe Zahl $\widehat {z}$ gilt: $\widehat {z}=x+iy$ , wobei $x$ der Realteil und $y$ der Imaginärteil ist.

Es gelten folgende Zusammenhänge:

$e^{ix}=cos \, x+i \, sin \, x$ Eulersche Formel (1748)

bzw.

$e^{i \varphi}=cos \, \varphi+i \, sin \, \varphi$ (Es gilt: $\varphi \, \in \, R$ )

Die Eulersche Formel stellt praktisch das Bindeglied zwischen trigonometrischen Funktionen und komplexen Zahlen dar.

Man kann komplexe Zahlen auch grafisch darstellen:

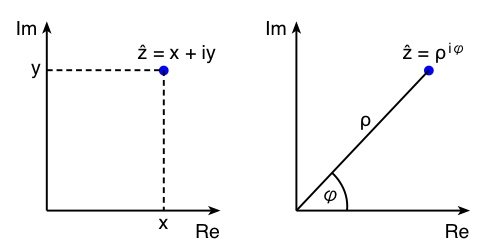
komplexe Zahlen grafische Darstellung

links: kartesisches Koordinatensystem rechts: Polarkoordinaten

Bei Polarkoordinaten wird der Abstand $\rho$ zum Ursprung und der Winkel $\varphi$ gegenüber der x-Achse angegeben.

Es gilt: $\rho=\sqrt {x^{2}+y^{2}}$ und $tan \varphi=\dfrac {y}{x}$

und damit umgekehrt: $x=\rho\cdot cos \varphi$ und $y=\rho \cdot sin \varphi$

Wichtig für uns ist:

Die komplexe e-Funktion ist eine nützliche Alternative zu trigonometrischen Funktionen und stellt in den folgenden Fällen die wesentlich einfachere Lösung dar.

(Man muss dafür nichts über komplexe Zahlen wissen, es reicht aus, sich an die Rechenvorschriften zu halten!)

Zusatzinfo:

Aus der Eulerschen Formel $e^{ix}=cos \, x+i \, sin \, x$ (s.o.) ergibt sich die sog. Eulersche Identität:

Für den Winkel $\varphi=180^{\circ}=\pi$ gilt:

$e^{i \pi}=-1$ Eulersche Identität

Diese Identität stellt einen verblüffend einfachen Zusammenhang zwischen den vier beteiligten mathematischen Konstanten $e,i,\pi$ und $1$ her.

Richard Feynman nannte diese Gleichung in seinem Notizbuch die „bemerkenswerteste Formel der Welt“, andere nennen sie die schönste Formel der Mathematik.

5. Operatoren und partielle Ableitungen

Ein Operator ist eine Rechenvorschrift, die auf das, was hinter dem Operator steht, angewendet werden soll.

Beispiele:

1. Die Funktion $f(x)$ soll nach $x$ abgeleitet werden.

Dies lässt sich schreiben als $f'(x)$ oder alternativ als $\dfrac {d}{dx}\, f(x)$ .

Die zweite Ableitung lässt sich schreiben als $f''(x)$ oder alternativ als $\dfrac {d^{2}}{dx^{2}}\, f(x)$ .

2. Die Funktion $s(t)$ soll zwei mal nach $t$ abgeleitet werden.

Dies lässt sich schreiben als $\ddot {s}(t)$ oder alternativ als $\dfrac {d^{2}}{dt^{2}}\, s(t)$

Diese Schreibweise haben wir bereits oben benutzt.

Partielle Ableitungen

Oft hängen Größen nicht nur von einer, sondern von mehreren Variablen ab. So kann der Funktionswert (z.B. eines Kraftfeldes) von allen drei Raumkoordinaten $x,y,z$ sowie von der Zeit $t$ abhängen. Will man eine solche Funktion ableiten, dann stellt sich die Frage: Nach welcher Variablen soll die Funktion abgeleitet werden?

Die Funktion $f(x,y,z)$ lässt sich sowohl nach $x$ , $y$ oder $z$ ableiten.

Leitet man eine Funktion nur nach einer Variablen ab, so spricht man von einer partiellen Ableitung.

Die Rechenvorschrift für eine partielle Ableitung nach $x$ wird geschrieben als $\dfrac {\partial}{\partial x}\, f(x,y,z)$ .

Genauso könnte man die Funktion nach $y$ oder $z$ ableiten. Die Rechenvorschriften dafür lauten entsprechend

$\dfrac {\partial}{\partial y}f(x,y,z)$ und $\dfrac {\partial}{\partial z}f(x,y,z)$

Bei einer partiellen Ableitung nach einer Variablen werden alle anderen Variablen (nach denen Du nicht ableitest) wie Konstanten behandelt.

Der Nabla-Operator $\nabla$

Der sog. Nabla-Operator ordnet einer Funktion die erste Ableitungsfunktion zu. Das Formelzeichen dieses Operators ist das Symbol $\nabla$ oder auch $\overrightarrow {\nabla}$ . Es handelt sich formal um einen Vektor, dessen Komponenten die partiellen Ableitungen sind.

Es gilt:

$\nabla f(x)=\dfrac {\partial}{\partial x}f(x)$ (Der Funktion $f(x)$ wird ihre erste Ableitungsfunktion zugeordnet)

Für den dreidimensionalen Raum gilt:

$\nabla=\left(\dfrac {\partial}{\partial x},\dfrac {\partial}{\partial y},\dfrac {\partial}{\partial z}\right)$

Wenn der Nabla-Operator vor einer Funktion steht, bedeutet das also, man soll die Funktion dahinter nach allen Variablen (partiell) ableiten.

Der Laplace-Operator $\Delta$

Der Laplace-Operator ordnet einer Funktion die zweite Ableitungsfunktion zu.

Es gilt die Beziehung: $\nabla ^{2}\equiv\Delta$

Es gilt:

$\Delta f(x)=\dfrac {\partial ^{2}}{\partial x ^{2}} f(x)$ (Der Funktion $f(x)$ wird ihre zweite Ableitungsfunktion zugeordnet.)

Für den dreidimensionalen Raum gilt:

$\nabla ^{2}f(x,y,z)=\Delta f(x,y,z)=\dfrac {\partial ^{2}}{\partial x ^{2}}f(x,y,z)+\dfrac {\partial ^{2}}{\partial y ^{2}}f(x,y,z)+\dfrac {\partial ^{2}}{\partial z ^{2}}f(x,y,z)$

Also ist $\Delta =\left(\dfrac {\partial ^{2}}{\partial x ^{2}}+\dfrac {\partial ^{2}}{\partial y ^{2}}+\dfrac {\partial ^{2}}{\partial z ^{2}}\right)$ der Laplace-Operator für den dreidimensionalen Fall.

Wie wir sehen, ist die Schreibweise mit Operatoren wesentlich kürzer und eleganter als wenn man jede Rechenvorschrift komplett ausschreibt.

Der Hamilton-Operator $\widehat{H}$

Ein weiterer in der Mechanik oder Quantenphysik gebräuchlicher Operator ist der Hamilton-Operator $\widehat{H}$ . Dabei handelt es sich um einen Energieoperator, der z.B. die Energiezustände im Atom liefert. Wie andere Operatoren wird er auf die dahinter stehende Funktion angewendet.

Der Hamilton-Operator enthält Funktionen für die kinetische und potentielle Energie und lässt sich schreiben als

$\widehat{H}= -\dfrac {\hbar^{2}}{2m} \Delta +V$ bzw. $\widehat{H}= -\dfrac {\hbar^{2}}{2m} \nabla ^{2}+V$

Dabei beschreibt $-\dfrac {\hbar^{2}}{2m} \nabla ^{2}$ die kinetische Energie und $V$ das Potential (potentielle Energie).

Die Konstante $\hbar$ (gesprochen: h quer, auch als reduziertes Plancksches Wirkungsquantum bezeichnet) ist nichts anderes als die Plancksche Konstante geteilt durch $2\pi$ : $\hbar=\dfrac {h}{2\pi}$